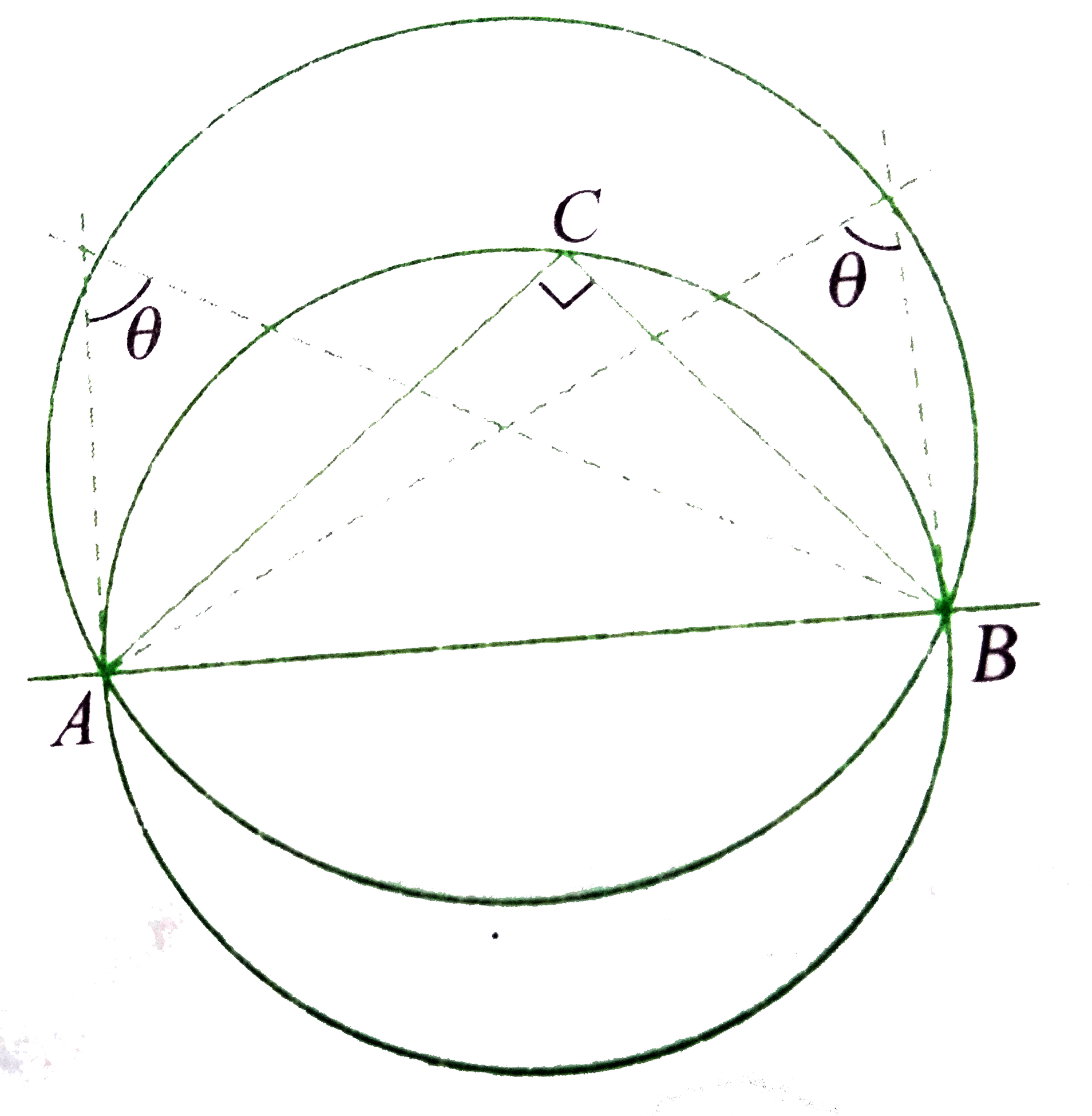
AandB are two points in the xy-plane, which are 2√2 units distance apart and subtend an angle of 900 at the point C(1,2) on the line x−y+1=0 , which is larger than any angle subtended by the line segment AB at any other point on the line. Find the equation(s) of the circle through the points A,BandC.Solution in Bengali
AB subtends the greatest angle at C, SO, theline x−y+1=0 touches the circle at C and, hence, AB is the diameter.
The family of circles touching the line
x−y+1=0 at point (1,2) is (x−1)2+(y−2)2+λ(x−y+1)=0
Its radius is
√(λ−22)2+(λ+42)2−(5+λ)=√2
or λ=±2
Therefore, the equations of the circles are
x2y2−6y+7=0
and x2+y2−4x−2y+3=0
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.11videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.22videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 42videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
04:03View SolutionFind the equation of the circle which touches the x-axis and whose center is (1, 2).
02:16View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
05:53View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:44View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is02:51View SolutionAandB are two points in the xy-plane, which are 2√2 units distance apart and subtend an angle of 900 at the point C(1,2) on the line x−y+1=0 , which is larger than any angle subtended by the line segment AB at any other point on the line. Find the equation(s) of the circle through the points A,BandC.
04:03View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects these lines at points PandQ . Then the angle subtended by the arc PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
05:31View SolutionIf a line segment joining two points subtends equal angles at two other points lying on the same side of the line segment; the four points are concyclic.
View SolutionFind the equation of the circle in which the chord joining the points (a,b) and (b,-a) subtends an angle of 45^(@) at any point on the circumference of the circle.
05:34View SolutionFind the locus of a point at which the angle subtended by the line segment joining (1,2)and(−1,3) is a right angle.
08:08View SolutionIf the line segment joining two points subtends equal angles at two other points on the same side, then the points are ………..
03:11View Solutionयदि दो बिंदुओं को मिलाने वाला रेखाखंड, उसको अंतर्विष्ट करने वाली रेखा के एक ही ओर स्थित दो अन्य बिंदुओं पर समान कोण अंतरित करे, तो चारों बिंदु एक वृत्त पर स्थित होते हैं (अर्थात वे चक्रीय होते हैं)।
02:17View SolutionTwo pillars of height a and b subtend the same angle alpha at a point on the line joining their feet. If the pillars subtend angles beta and gamma at another point in the horizontal plane at which the line joining their feet subtends a right angle then,
01:47View SolutionAandB are two points in the xy-plane, which are 2√2 units distance apart and subtend an angle of 900 at the point C(1,2) on the line x−y+1=0 , which is larger than any angle subtended by the line segment AB at any other point on the line. Find the equation(s) of the circle through the points A,BandC.
04:18View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects these lines at points PandQ . Then the angle subtended by the arc PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
08:51View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects there lines at points PandQ . Then the angle subtended by the are PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
05:33View Solution