AB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
To prove that point F is the midpoint of line segment BC in trapezium ABCD, where AB is parallel to CD and E is the midpoint of AD, we will follow these steps:
Step 1: Understand the trapezium and the given points
- We have trapezium ABCD with AB || CD.
- E is the midpoint of AD, which means AE = ED.
Hint: Identify the properties of trapeziums and the significance of midpoints in geometry.
Step 2: Draw a line through E parallel to AB
- Draw a line EF through point E such that EF || AB. By the properties of parallel lines, we know that corresponding angles will be equal.
Hint: Remember that parallel lines create equal alternate interior angles.
Step 3: Identify the intersection point F
- Let line EF intersect line BC at point F. Now we have established that EF is parallel to AB.
Hint: Use the properties of parallel lines and transversals to analyze the angles formed.
Step 4: Apply the Midpoint Theorem
- In triangle ACD, since E is the midpoint of AD and EF is parallel to CD, by the Midpoint Theorem, we can conclude that F is the midpoint of BC.
Hint: The Midpoint Theorem states that a line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
Step 5: Conclude the proof
- Since F is the midpoint of BC, we have proved that F divides BC into two equal segments, thus confirming that F is indeed the midpoint of line segment BC.
Hint: Summarize your findings and relate them back to the properties of trapeziums and midpoints.
Final Conclusion:
Therefore, we have shown that point F is the midpoint of BC in trapezium ABCD.
- We have trapezium ABCD with AB || CD.
- E is the midpoint of AD, which means AE = ED.
- Draw a line EF through point E such that EF || AB. By the properties of parallel lines, we know that corresponding angles will be equal.
- Let line EF intersect line BC at point F. Now we have established that EF is parallel to AB.
- In triangle ACD, since E is the midpoint of AD and EF is parallel to CD, by the Midpoint Theorem, we can conclude that F is the midpoint of BC.
- Since F is the midpoint of BC, we have proved that F divides BC into two equal segments, thus confirming that F is indeed the midpoint of line segment BC.
Therefore, we have shown that point F is the midpoint of BC in trapezium ABCD.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
ABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
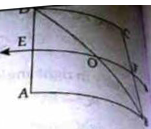
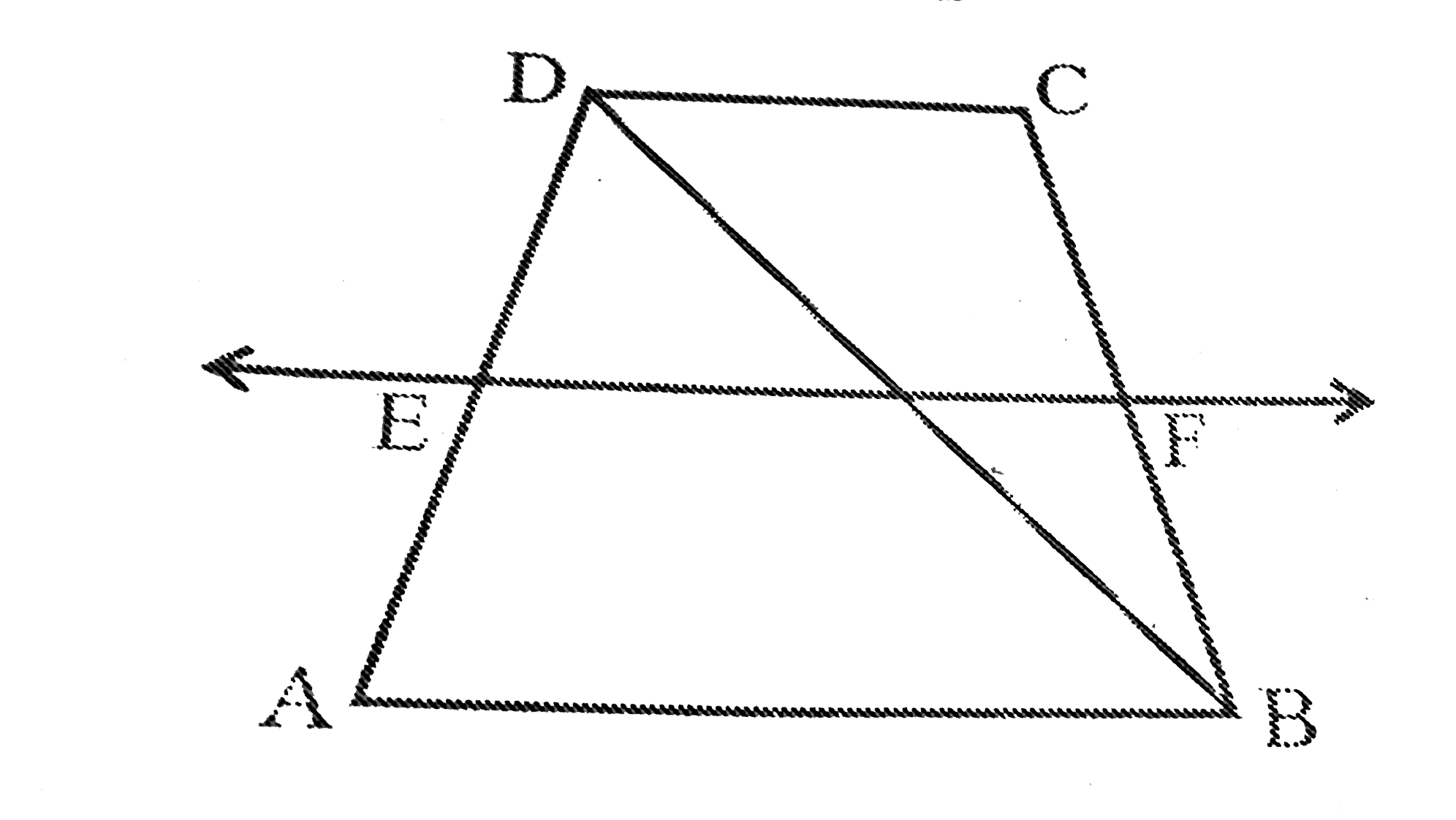
View SolutionABCD is a trapezium in which AB ∣∣ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
View Solution
Knowledge Check
E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
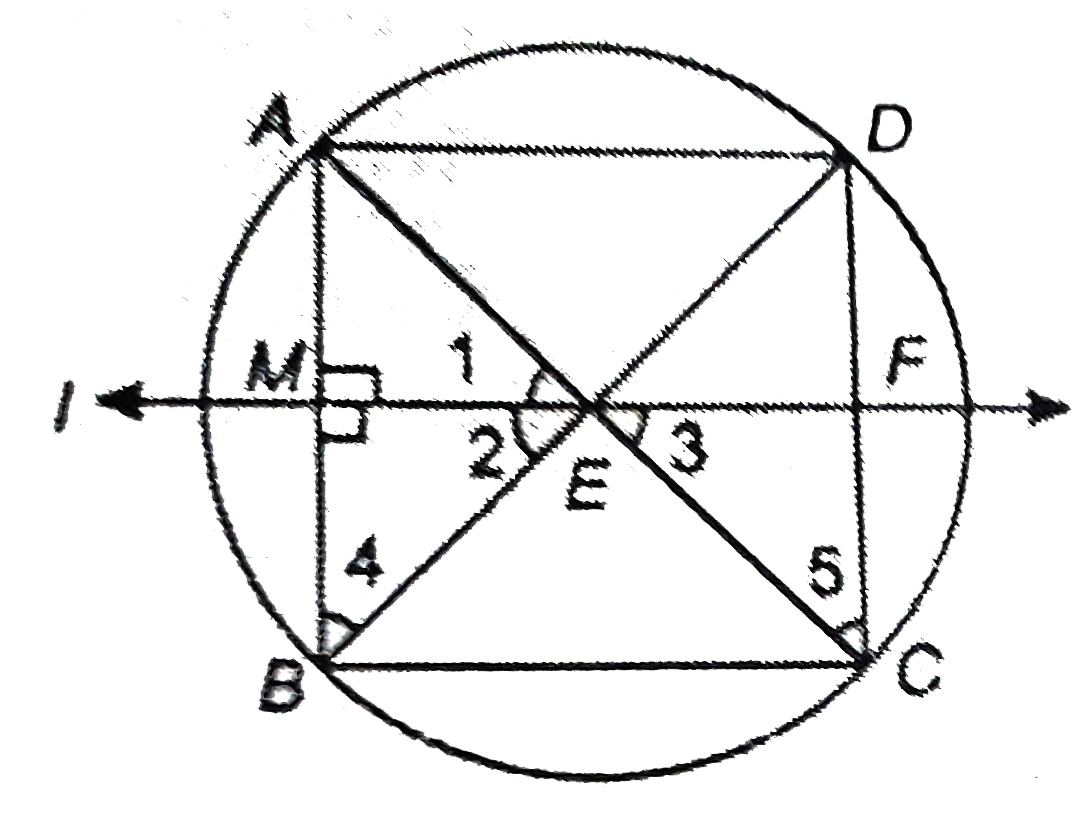
The diagonals AC and BD of a cyclic quadrilateral ABCD interest at right angles at E (figure). A line l drawn through E and perpendicular to AB meets CD at F. Prove that F is the mid-point of CD.
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
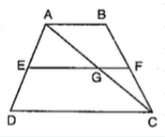
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionThe line drawn through the mid-point of one side of a triangle, parallel to another side, intersects the third side at its mid-point.
View SolutionThe line drawn through the mid-point of one side of a triangle is parallel to another side and intersects the third side at its mid-point.
View SolutionThe line joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View Solution
