The line joining the mid-points of two sides of a triangle is parallel to the third side.
To prove that the line joining the midpoints of two sides of a triangle is parallel to the third side, we can follow these steps:
1. Identify the Triangle and Midpoints:
Let triangle ABC be given. Let D be the midpoint of side AB and E be the midpoint of side AC.
Hint: Remember that the midpoint of a line segment divides it into two equal parts.
2. Define the Lengths:
Since D is the midpoint of AB, we have AD = DB. Similarly, since E is the midpoint of AC, we have AE = EC.
Hint: Use the property of midpoints to express the lengths of the segments.
3. Set Up Ratios:
From the above definitions, we can write the ratios:
ADDB=1andAEEC=1
Hint: The ratios indicate that both segments are equal.
4. Apply the Basic Proportionality Theorem:
Since we have:
ADDB=AEEC
This is in the form required by the Basic Proportionality Theorem (also known as Thales' theorem), which states that if a line divides two sides of a triangle proportionally, then it is parallel to the third side.
Hint: Recall the Basic Proportionality Theorem and how it relates to parallel lines.
5. Conclude the Proof:
By the Basic Proportionality Theorem, since the ratios are equal, we conclude that line DE (the line joining midpoints D and E) is parallel to side BC.
Hint: Use the conclusion from the theorem to finalize your proof.
Final Statement:
Thus, we have proved that the line joining the midpoints of two sides of a triangle is parallel to the third side.
Let triangle ABC be given. Let D be the midpoint of side AB and E be the midpoint of side AC.
Since D is the midpoint of AB, we have AD = DB. Similarly, since E is the midpoint of AC, we have AE = EC.
From the above definitions, we can write the ratios:
ADDB=1andAEEC=1
Since we have:
ADDB=AEEC
This is in the form required by the Basic Proportionality Theorem (also known as Thales' theorem), which states that if a line divides two sides of a triangle proportionally, then it is parallel to the third side.
By the Basic Proportionality Theorem, since the ratios are equal, we conclude that line DE (the line joining midpoints D and E) is parallel to side BC.
Thus, we have proved that the line joining the midpoints of two sides of a triangle is parallel to the third side.
Similar Questions
Knowledge Check
Assertion : If a line divides any two sides of a triangle in the same ratio , then the line is paralle to third side .
Reason : Line segment joining the mid -point of any two sides of a triangle is parallel to the third side .AIf both assertion and reason are true and reason is the correct explanation of assertion .BIf both assertion and reason are true but reason is not the correct explanation of assertion .CIf assertion is true reason is false .DIf assertion is false but reason is true .Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC. Then DP = PC.
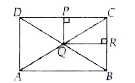
Reason : The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
In the given figure, the side AC of ΔABC is produced to E such that CE = FAC. If D is the midpoint of BC and ED produced meets AB at F and CP, DQ are drawn parallel to BA, then FD=
 A12FEB13EFC2FEDFE
A12FEB13EFC2FEDFE
prove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionThe line segment joining the mid-points of any two sides of a triangle is parallel to the third side of a triangle.
View SolutionProve that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionThe line segment joining the mid-points of any two sides of a triangle in parallel to the third side and equal to half of it.
View SolutionProve that the line joining the middle points of the two sides of a triangle is parallel to the third side.
View Solution
