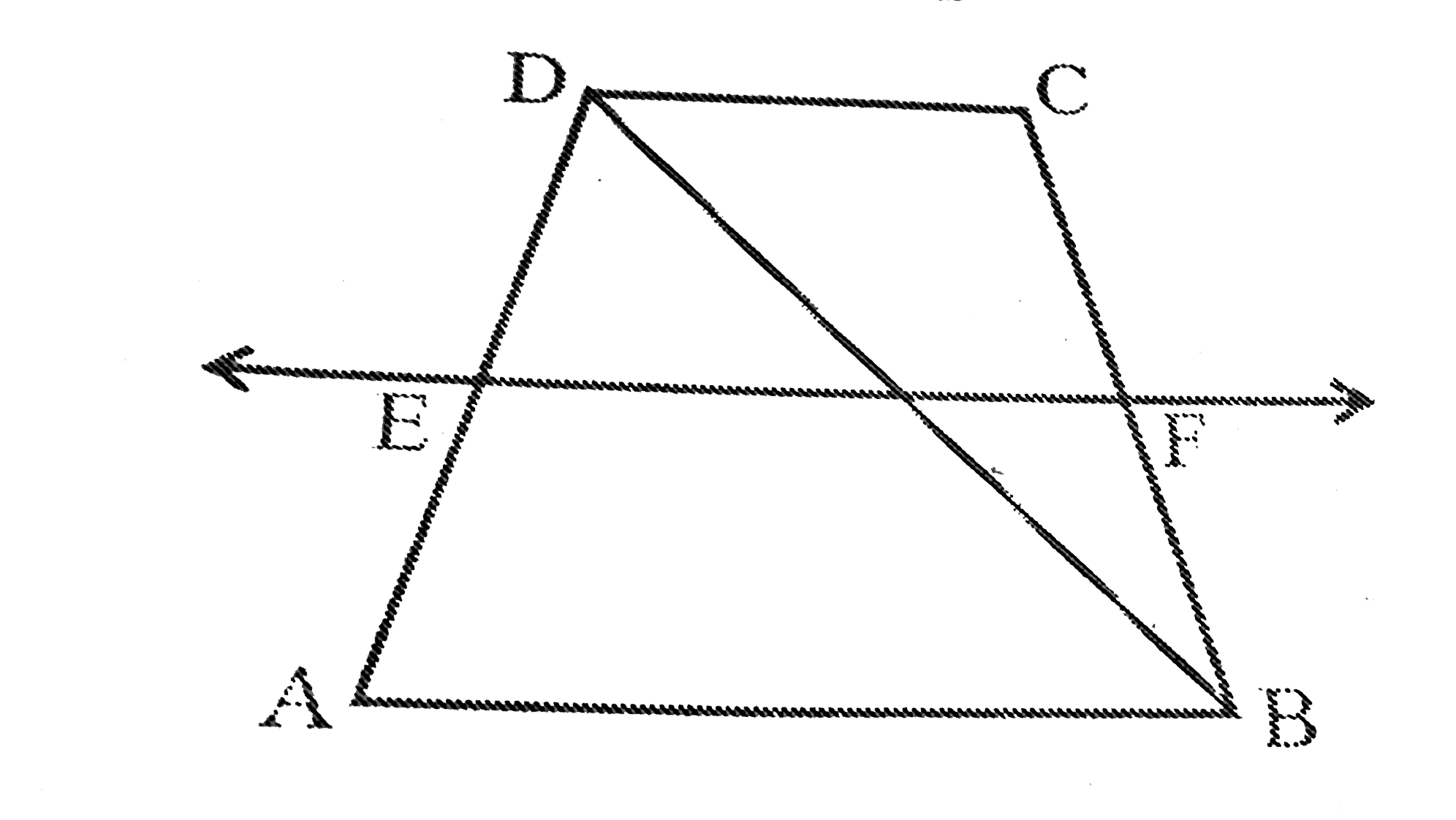
AB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
To prove that point F is the midpoint of line segment BC in trapezium ABCD, where AB and CD are the parallel sides, and E is the midpoint of AD, we will follow these steps:
Step 1: Draw the trapezium and construct the line
- Draw trapezium ABCD with AB || CD.
- Mark E as the midpoint of AD.
- Draw a line through E that is parallel to AB, which intersects BC at point F.
Hint: Remember that parallel lines maintain the same distance apart and do not intersect.
Step 2: Join points D and B
- Join points D and B to form line DB.
Hint: This line will help us analyze the triangles formed in the trapezium.
Step 3: Identify triangle ADB
- Consider triangle ADB. Since E is the midpoint of AD, we can denote AE = ED.
Hint: Midpoints divide a segment into two equal parts.
Step 4: Apply the Midpoint Theorem
- Since EF is parallel to AB and E is the midpoint of AD, by the Midpoint Theorem, point O (the intersection of line DB and line EF) must be the midpoint of DB.
Hint: The Midpoint Theorem states that a line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length.
Step 5: Analyze triangle DBC
- Now, consider triangle DBC. We know that O is the midpoint of DB and EF is parallel to DC.
Hint: Since EF is parallel to both AB and DC, the properties of parallel lines apply.
Step 6: Conclude that F is the midpoint of BC
- By the converse of the Midpoint Theorem, since O is the midpoint of DB and EF is parallel to DC, F must be the midpoint of BC.
Hint: The converse of the Midpoint Theorem states that if a line segment is drawn parallel to one side of a triangle and intersects the other two sides, it divides those sides proportionally.
Final Conclusion
Thus, we have proved that F is the midpoint of BC.
- Draw trapezium ABCD with AB || CD.
- Mark E as the midpoint of AD.
- Draw a line through E that is parallel to AB, which intersects BC at point F.
- Join points D and B to form line DB.
- Consider triangle ADB. Since E is the midpoint of AD, we can denote AE = ED.
- Since EF is parallel to AB and E is the midpoint of AD, by the Midpoint Theorem, point O (the intersection of line DB and line EF) must be the midpoint of DB.
- Now, consider triangle DBC. We know that O is the midpoint of DB and EF is parallel to DC.
- By the converse of the Midpoint Theorem, since O is the midpoint of DB and EF is parallel to DC, F must be the midpoint of BC.
Thus, we have proved that F is the midpoint of BC.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionE is the mid-point of the side AD of the tarapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-points of BC.
View SolutionABCD is a trapezium in which AB ∣∣ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.
View SolutionIn a triangle ABC, AD is a medium and E is mid-point of median AD. A line through B and E meets AC at point F.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if EF=4.8cm.
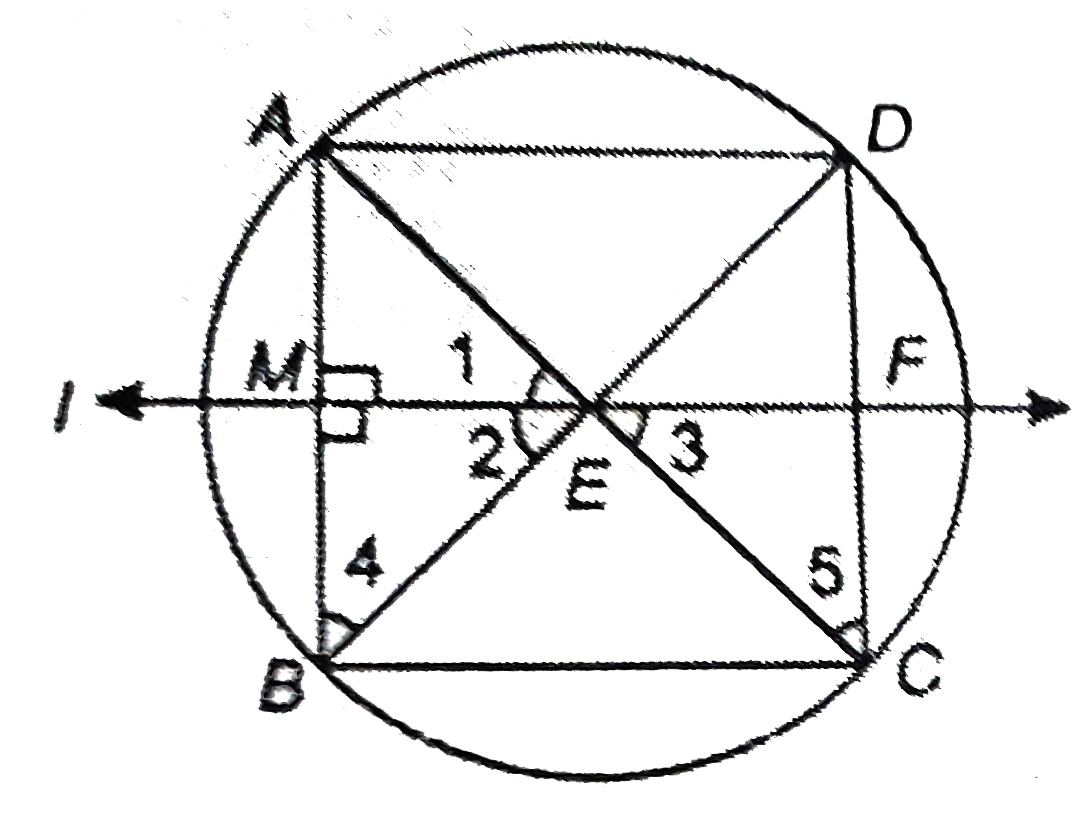
View SolutionThe diagonals AC and BD of a cyclic quadrilateral ABCD interest at right angles at E (figure). A line l drawn through E and perpendicular to AB meets CD at F. Prove that F is the mid-point of CD.
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View Solution
