AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is
1819
319
16
13
On the basis of the given information , following diagram is obtained .
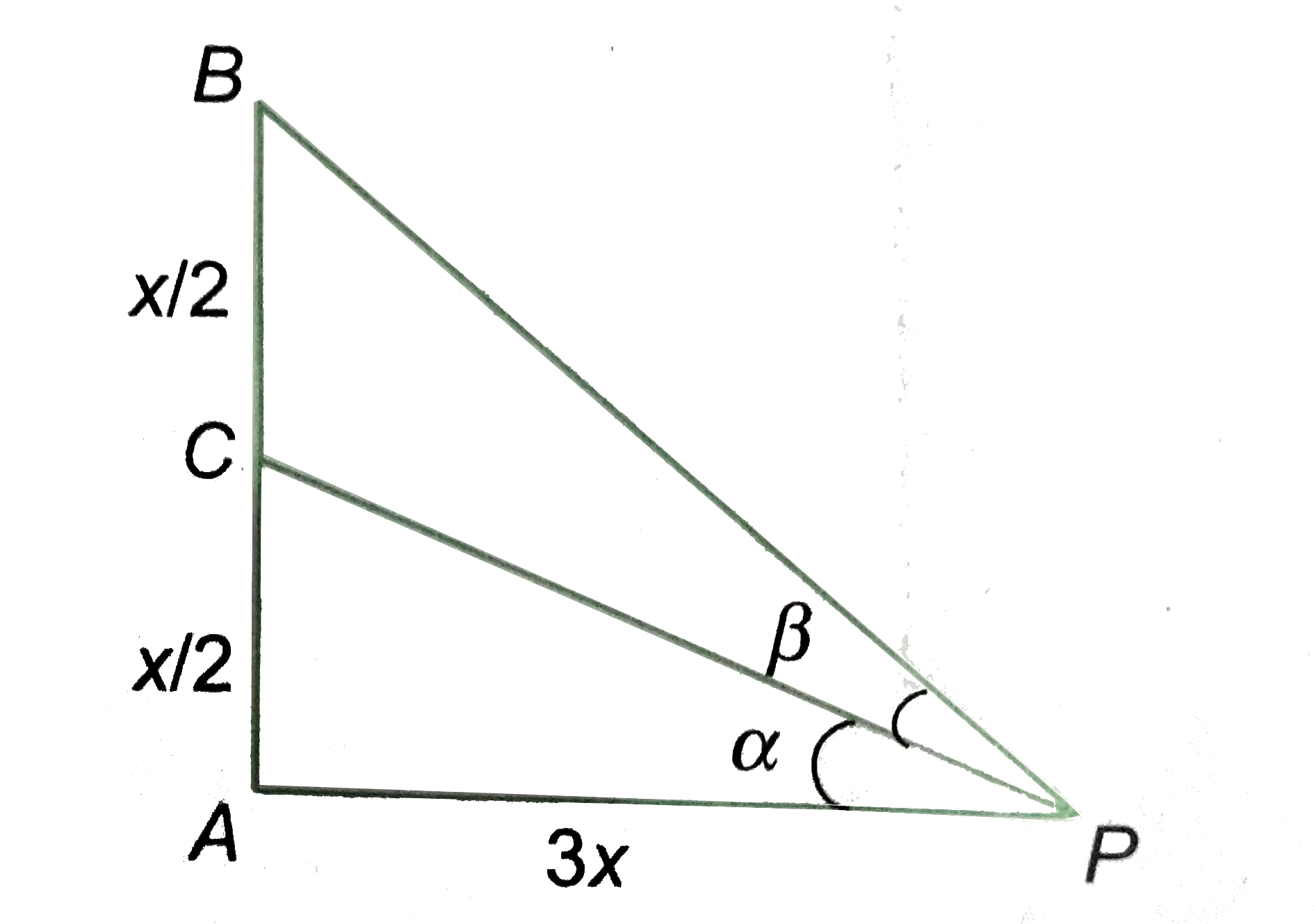
tanβ=tan((α+β)−α)
=13−161+13.16=319
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- HYPERBOLABOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
Similar Questions
AB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View Solution
Knowledge Check
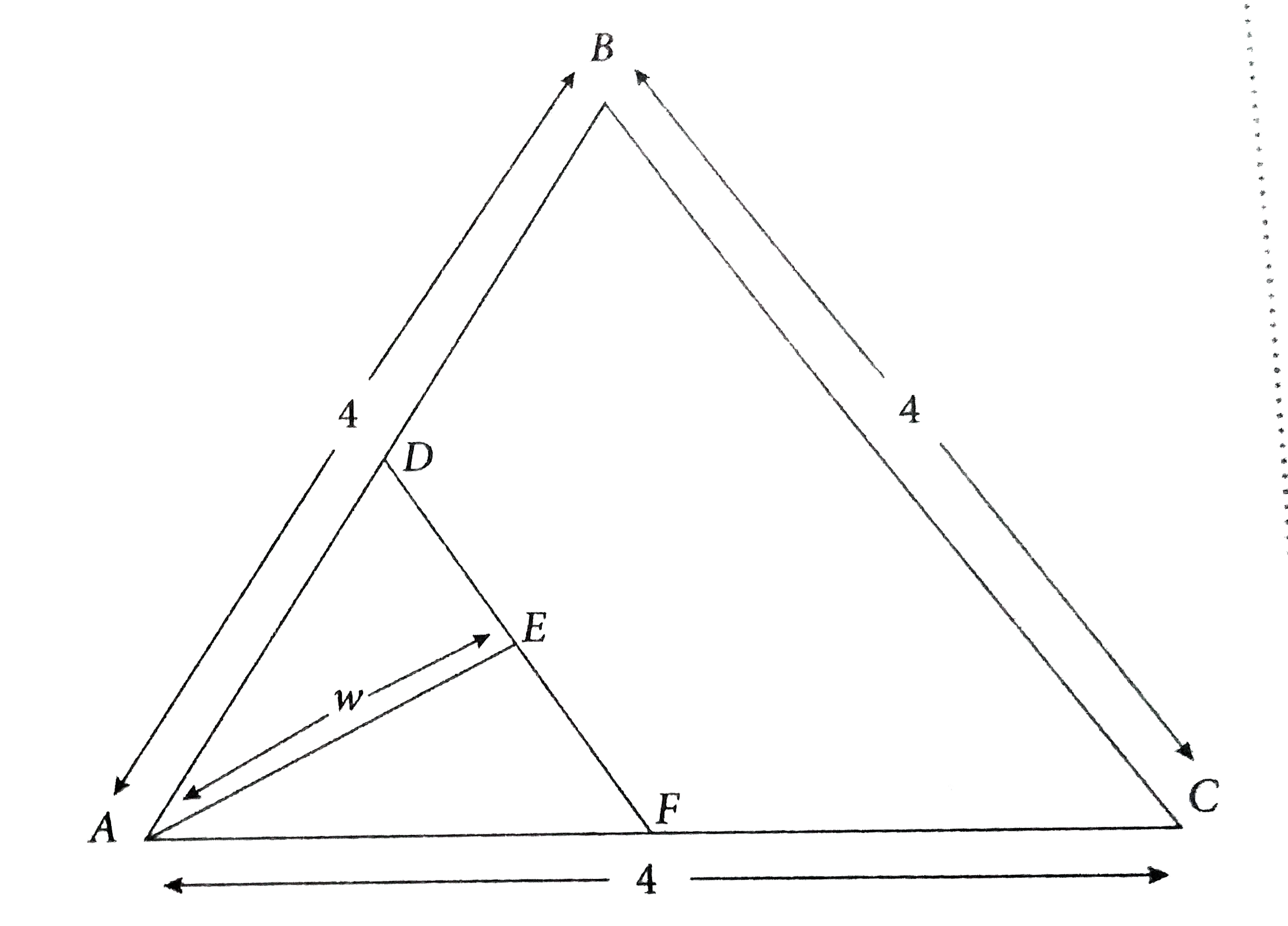
ΔABC is equilateral and ∠AEF is a right angle . D and F are the midpoints of AB and AC, respectively. What is the value of w?A1B√3C2D2√3
AB is vertical tower. The point A is on the ground and C is the middle point of AB. The part CB subtend an angle α at a point P on the ground. If AP=nAB, then tanα=
View SolutionIf →a & →b are the position vectors of A & B respectively and C is a point on AB produced such that AC=3AB then the position vector of C is:
View SolutionIf the coordinates of midpoints of ABandACofΔ A B C are (3,5) and (-3,-3) respectively, then write the length of side BC.
View SolutionIf A=(2, -3, 7), B = (-1, 4, -5) and P is a point
on the line AB such that AP:BP=3:2 then P
has the coordinates
View SolutionAt the point of intersection of the curves y2=4ax and xy=c2, the tangents to the two curves make angles α and β respectively with x-axis. Then tanαcotβ=
View SolutionLet a vertical tower AB have its end A on the level ground. Let C be the mid point of AB and P be a point on the ground such that AP=2AB. If ∠BPC=β, then tanβ is equal to : (1) 29 (2) 49 (3) 67 (4) 14
View SolutionThe angles of elevation of a cliff at a point A on the ground and at a point B 100 mt vertically above A are α are β respectively.The height of the cliff in metres is
View Solution
