ab−mn+an−bm = ?
(a−b)(m−n)
(a−m)(b+n)
(a−n)(m+b)
(m−a)(n−b)
The correct Answer is:B
To factor the expression ab−mn+an−bm, we can follow these steps:
1. Rearrange the expression:
We can rearrange the terms to group them in a way that makes factoring easier:
ab+an−mn−bm
2. Group the terms:
Now, we can group the first two terms and the last two terms:
(ab+an)+(−mn−bm)
3. Factor out the common factors:
- From the first group ab+an, we can factor out a:
a(b+n)
- From the second group −mn−bm, we can factor out −m:
−m(n+b)
Now, we rewrite the expression:
a(b+n)−m(n+b)
4. Notice that (n+b) can be rewritten:
Since (n+b) is the same as (b+n), we can rewrite the expression as:
a(b+n)−m(b+n)
5. Factor out the common binomial factor:
Now, we can factor out the common binomial (b+n):
(b+n)(a−m)
Thus, the final factored form of the expression ab−mn+an−bm is:
(b+n)(a−m)
We can rearrange the terms to group them in a way that makes factoring easier:
ab+an−mn−bm
Now, we can group the first two terms and the last two terms:
(ab+an)+(−mn−bm)
- From the first group ab+an, we can factor out a:
a(b+n)
- From the second group −mn−bm, we can factor out −m:
−m(n+b)
a(b+n)−m(n+b)
Since (n+b) is the same as (b+n), we can rewrite the expression as:
a(b+n)−m(b+n)
Now, we can factor out the common binomial (b+n):
(b+n)(a−m)
(b+n)(a−m)
Topper's Solved these Questions
- FACTORISATION BOOK - RS AGGARWALCHAPTER - FACTORISATION EXERCISE - EXERCISE 7D
42 Videos
- EXPONENTS BOOK - RS AGGARWALCHAPTER - EXPONENTS EXERCISE - TEST PAPER-2
18 Videos
- INTRODUCTION TO COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - INTRODUCTION TO COORDINATE GEOMETRYEXERCISE - EXERCISE B (OBJECTIVE QUESTIONS)
7 Videos
Similar Questions
Knowledge Check
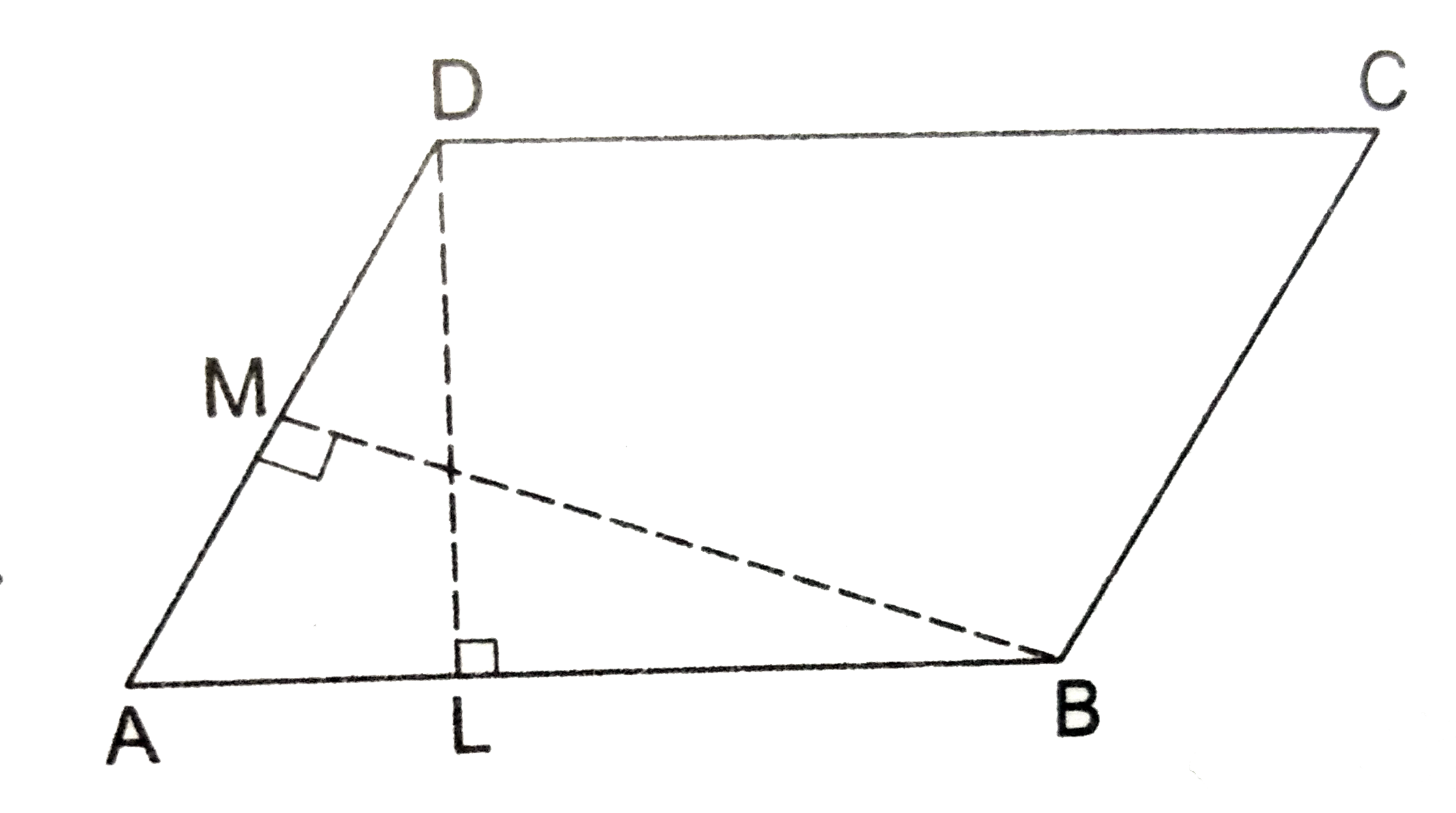
In the given figure, AB = 30 cm and CD = 24 cm. What is the value (in cm) of MN?
 A18B9C12D15
A18B9C12D15If the lengths of the sides AB, BC and CA of a triangle ABC are 10 cm, 8 cm and 6 cm respectively and if M is the mid-point of BC and MN || AB to cut AC at N, then the area of the trapezium ABMN is equal to
A(a) 18 sq. cmB(b) 20 sq. cmC(c) 12 sq. cmD(d) 16 sq. cmIn the given figure, ABCD is a trapezium such that AL⊥DCandBM⊥DC. If AB=7cm,BC=AD=5cm and AL=BM=4cm then ar(trap.ABCD)=?
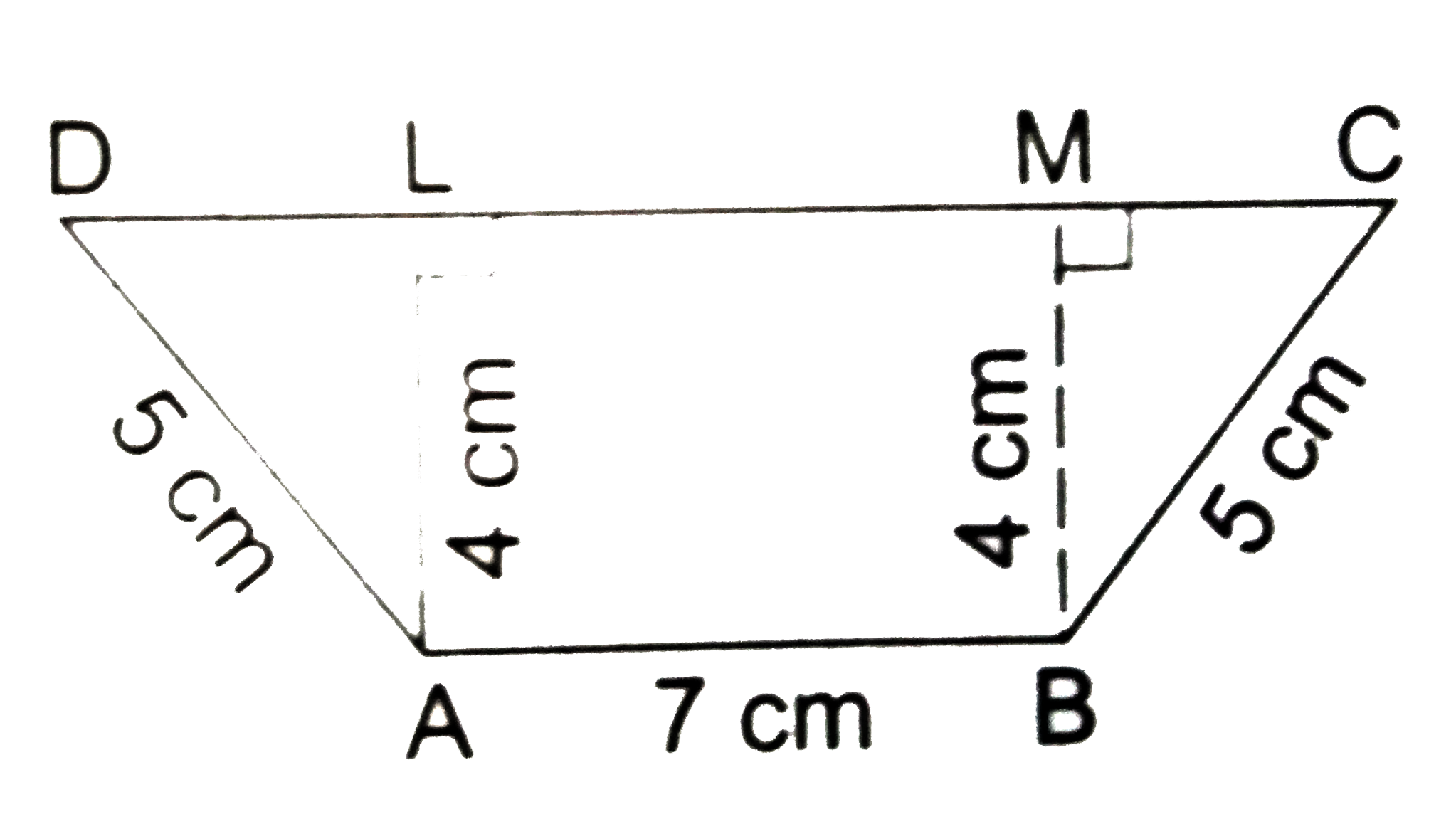 A24cm2B40cm2C55cm2D27.5cm2
A24cm2B40cm2C55cm2D27.5cm2
Add:
−7mn+5,12mn+2,9mn−8,−2mn−3
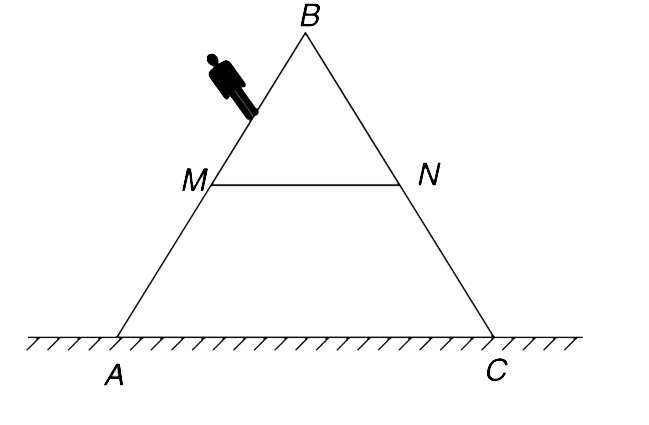
View SolutionThe ladder shown in the figure is light and stands on a frictionless horizontal surface. Arms AB and BC are of equal length and M and N are their mid points. Length of MN is half that of AB. A man of mass M is standing at the midpoint of BM. Find the tension in the mass less rod MN. Consider the man to be a point object.
View Solution∠ABC=90∘ and BM is a median AB=8cm and BC=6cm. Then, length BM is equal to
View SolutionA semi-circle has been drawn on AB as a diameter and two chords ALandBM have been draw there in which intersect each other a P. Prove that AB2=AL−AP+BM−BP.
View SolutionIt is given that in △ABC, M is midpoint of AC, circle of center B cuts AB and BC of D & E, BM cuts the chord DE at G. Here AB = 12, DG = 5, BC = 15, Find GE = ?

View Solution