ABC is any triagnel inscribed in the circle x2+y2=r2 such that A is fixed point . If the external and internal bisectors of ∠A intersect the circle at D and E, respectively, then which of the following statements is true ΔADE ?
Its centroid is a fixed point.
Its circumcentre is a fixed point.
Its orthocentre is a fixed point.
none of these
The correct Answer is:1,2,3
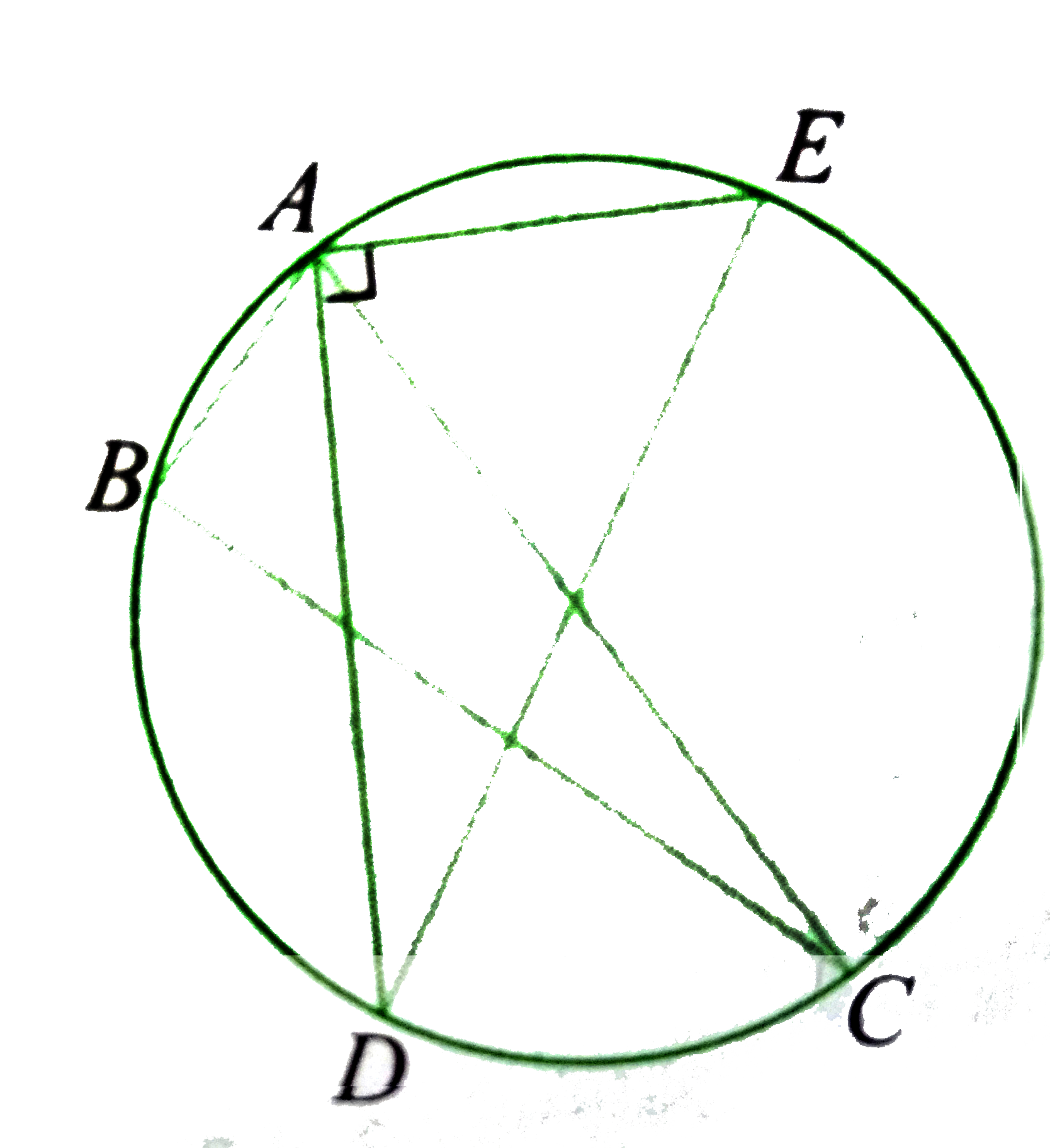
Orothocentre of ΔADE is A itself circumcentre is at origin. Hence, centroid is also a fixed point.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Single)
109 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
Knowledge Check
AD is the median of ABC and E is any point on AD. Which of the following statement is true ?
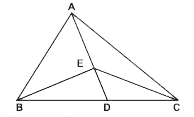 Aar (ΔABD)> ar (ΔACD)Bar (ΔABD)< ar (ΔACD)Car (ΔABE)= ar (ΔCED)Dar (ΔABE)= ar (ΔACE)
Aar (ΔABD)> ar (ΔACD)Bar (ΔABD)< ar (ΔACD)Car (ΔABE)= ar (ΔCED)Dar (ΔABE)= ar (ΔACE)Area of the equilateral triangle inscribed in the circle x2+y2−7x9y+5=0 is
A1558√3squnitsB1658√3squnitsC1758√3squnitsD1858√3squnitsIn a triangle ABC, internal bisector of ∠ABC and external bisector of ∠ACB meet in D. Which one of the following is true ?
A∠BDC=∠BACB∠BDC=12∠ABCC∠BDC=∠DBCDNone of these
Area of the equilateral △ inscribed in the circle x2+y2−7x+9y+5=0, is …………
View SolutionArea of the equilateral △ inscribed in the circle x2+y2−7x+9y+5=0, is …………
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A
View SolutionAn equilateral triangle is inscribed in the circle x2+y2=1 which one vertex at the point (1,0). Length of each side of the tringle is
View SolutionABCD is a quadrilateral inscribed in a circle (radius=r). The bisectors of the angles DAB and BCD intersect the circle at X and Y. respectively. What is the length of the straight line XY?
View Solution
