ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED=65∘ , Calculate
(i) ∠DAB
(ii) ∠BDC
The correct Answer is:(i)65∘(ii)25∘
To solve the problem step by step, we will analyze the cyclic quadrilateral ABCD with the given conditions.
1. Identify the Given Information:
- ABCD is a cyclic quadrilateral.
- AB is parallel to DC.
- AB is the diameter of the circle.
- Angle BED = 65°.
2. Use the Property of Angles Subtended by the Same Chord:
- Since AB is the diameter, angle DAB subtended by chord DB at point A is equal to angle BED (subtended at point E).
- Therefore, we have:
∠DAB=∠BED=65°
3. Determine Angle ADB:
- Since AB is the diameter of the circle, angle ADB (formed at point D) is a right angle (90°) because the angle in a semicircle is always 90°.
- Thus, we have:
∠ADB=90°
4. Find Angle ABD:
- In triangle ADB, we can find angle ABD using the fact that the sum of angles in a triangle is 180°.
- Therefore:
∠ADB+∠DAB+∠ABD=180°
- Substituting the known values:
90°+65°+∠ABD=180°
- Simplifying gives:
∠ABD=180°−90°−65°=25°
5. Use the Parallel Lines Property:
- Since AB is parallel to DC, angle ABD is equal to angle BDC (alternate interior angles).
- Therefore:
∠BDC=∠ABD=25°
Final Answers:
- (i) Angle DAB = 65°
- (ii) Angle BDC = 25°
- ABCD is a cyclic quadrilateral.
- AB is parallel to DC.
- AB is the diameter of the circle.
- Angle BED = 65°.
- Since AB is the diameter, angle DAB subtended by chord DB at point A is equal to angle BED (subtended at point E).
- Therefore, we have:
∠DAB=∠BED=65°
- Since AB is the diameter of the circle, angle ADB (formed at point D) is a right angle (90°) because the angle in a semicircle is always 90°.
- Thus, we have:
∠ADB=90°
- In triangle ADB, we can find angle ABD using the fact that the sum of angles in a triangle is 180°.
- Therefore:
∠ADB+∠DAB+∠ABD=180°
- Substituting the known values:
90°+65°+∠ABD=180°
- Simplifying gives:
∠ABD=180°−90°−65°=25°
- Since AB is parallel to DC, angle ABD is equal to angle BDC (alternate interior angles).
- Therefore:
∠BDC=∠ABD=25°
- (i) Angle DAB = 65°
- (ii) Angle BDC = 25°
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
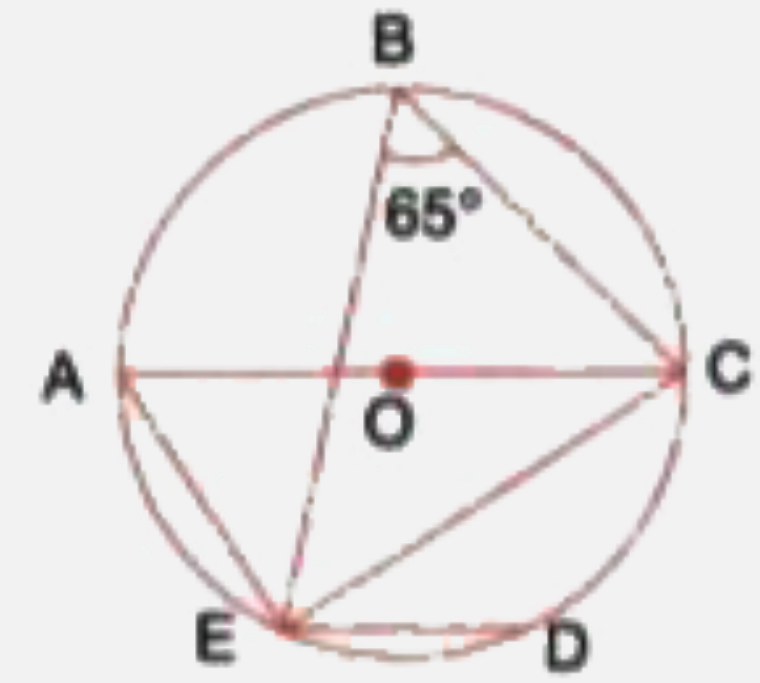
In the given figures, chord ED is parallel to diameter AC of the circle . Given ∠CBE=65∘ calculate ∠DEC
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
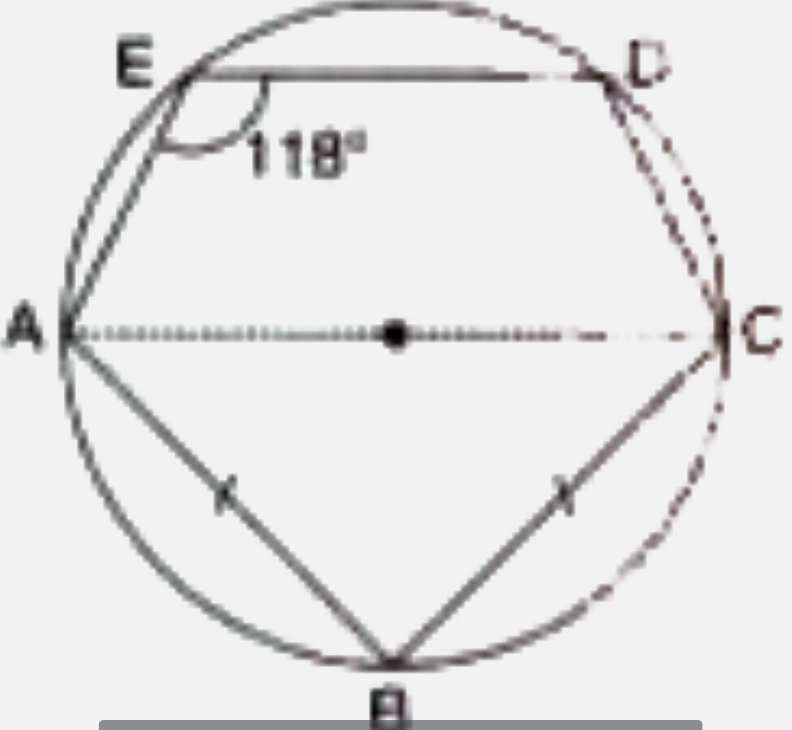
View SolutionIn the adjoining figure, AC is diameter of the circle AB = BC and ∠AED=118∘. Calculate :
∠DEC
View SolutionABCD is a cyclic quadrilateral in which BC is paralleld to AD, angle ADC=110∘ and angle BAC=50∘. Find angle DAC and angle DCA.
View SolutionIn the given figure ABCD is a cyclic quadrilateral in which AE is drawn parallel to CD and BA is produced. If ∠ABC=92∘ and ∠FAE=20∘, Find ∠BCD.

View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionIn the following figure , ABCD is a cyclic quadrilateral in which AD is parallel to BC .
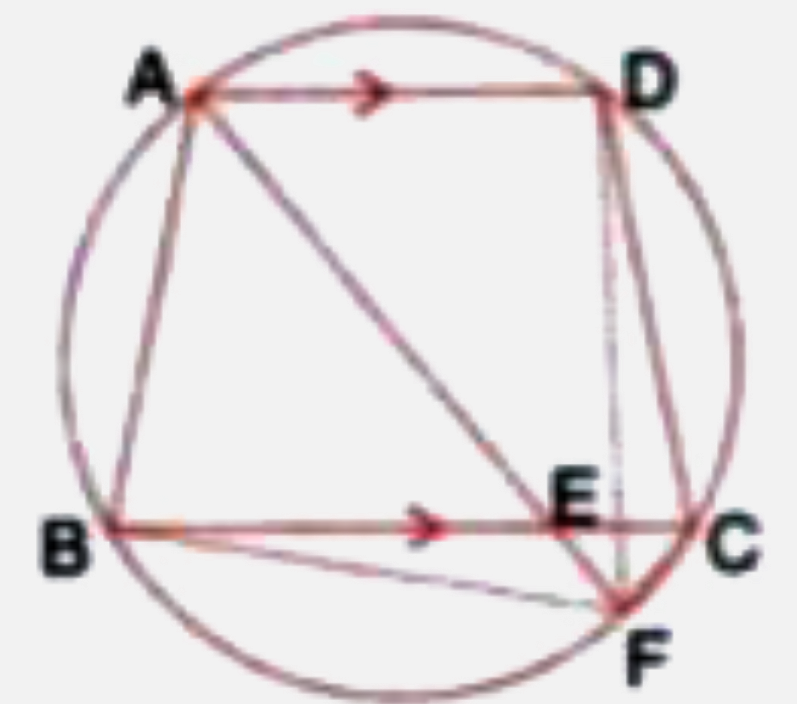
If the bisector of angle A meets BC at point E and given circle at point F, prove that :
(i) EF =FC
(ii) BF = DF
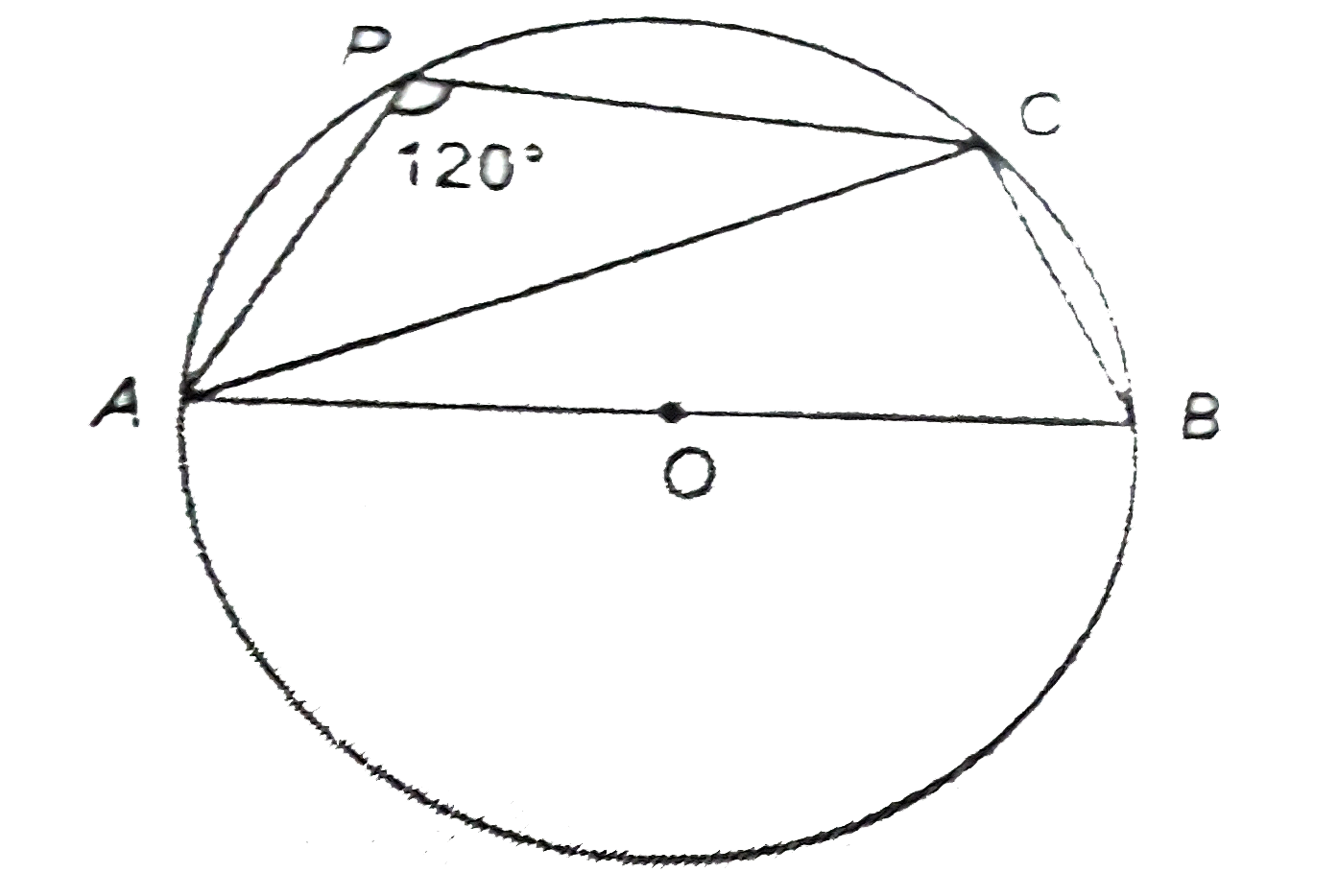
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED

View Solution
