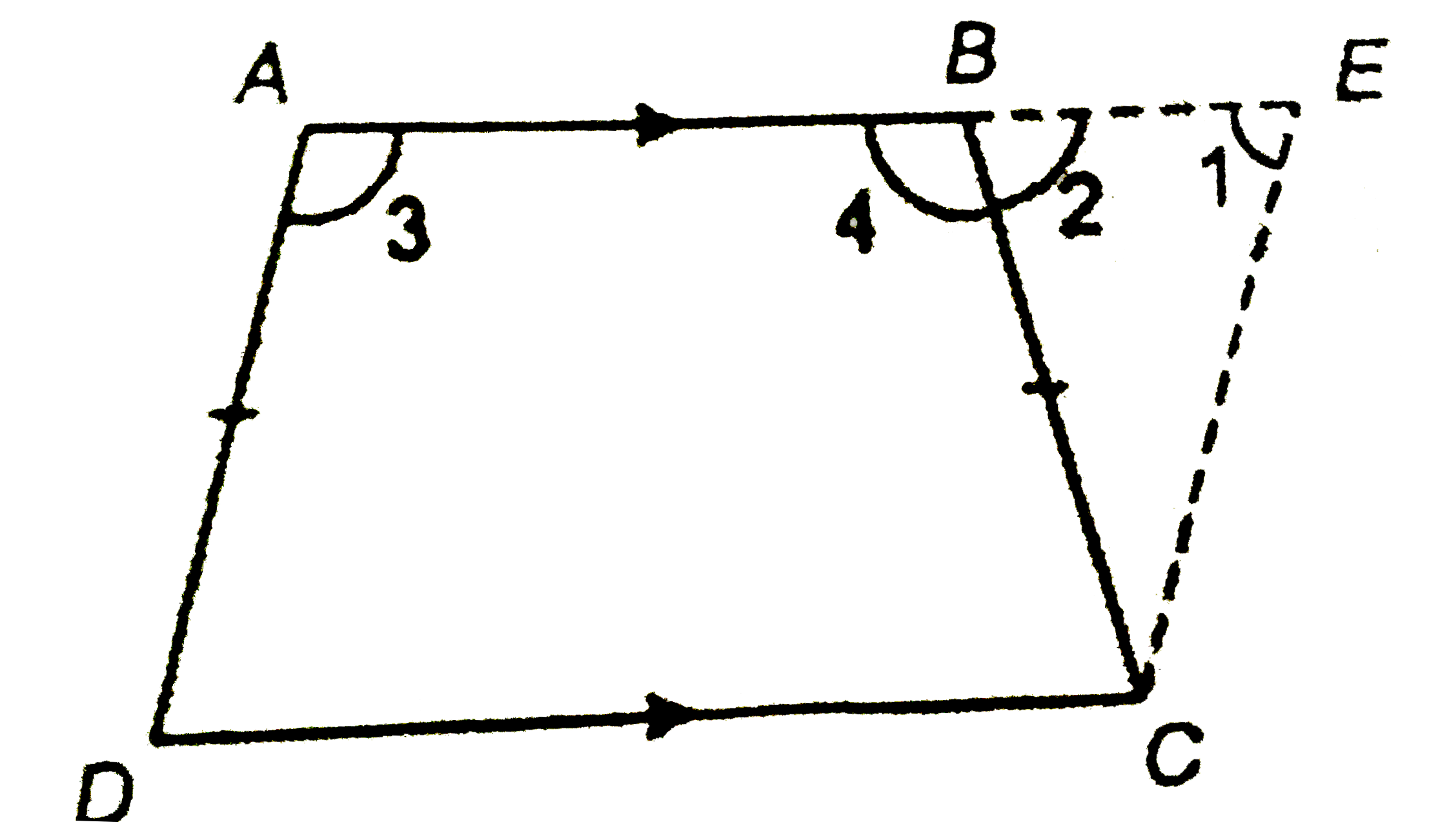
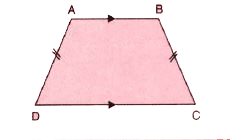
ABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
Draw CE \\\\ AD from point C with meets AB produced at E.
Now,AB||DC===⇒AE||DC
In □AECD.
AE||DCandAD||EC
∴□AECDis a parallelogram. (∵pairof opposite sides are parallel)
⇒ AD=CE (opposite sides of a parallelogram)
and ∠A+∠E=180∘ (sumof co-interio angles)
But AD=BC (given)
∴ BC=CE
⇒ ∠1=∠2 (angles opposite to equal sides are equal)
Now, ∠1+∠3=180∘ (sum of co-interior angles)
Also, ∠2+∠4=180∘ (L.P.A.)
∴ ∠1+∠3=∠2+∠4
⇒ ∠3=∠4 (∵∠1=∠2)
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
Find ∠A+∠B+∠C+∠D
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
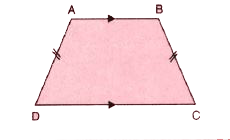
∠C=∠D
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
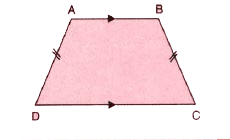
∠A=∠B
View SolutionIn quadrilateral ABCD, AD = BC and BD = CA. Prove that :
(i) ∠ADB=∠BCA
(ii) ∠DAB=∠CBA
View SolutionThe following figure shows a quadrilateral in which sideo AB and DC are parallel. If ∠A:∠D=4:5,∠B=(3x−15)∘and∠C=(4x+20)∘, find each angle of the quadrilateral ABCD.

View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC bisects angle BAD
View SolutionBisectors of angles A and D of a quadrilateral ABCD meet at P. Prove that ∠APD=12(∠B+∠C)
View SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
Diagonal AC= diagonal BD
View Solution
