Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

Step by step video & image solution for Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
Show that the bisectors of angles of a parallelogram form a rectangle.
View SolutionShow that the bisectors of angles of a parallelogram form a rectangle.
View SolutionTwo parallel lines l and m are intersected by a transversal p . Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionThe angle bisectors of a parallelogram form a rectangle.
View SolutionProve that the bisectors of opposite angles of a parallelogram are parallel.
View Solution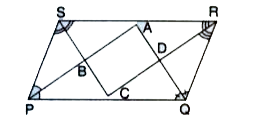
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) ∠PSB+∠SPB=90∘
(ii) ∠PBS=90∘
(iii) ∠ABC=90∘
(iv) ∠ADC=90∘
(v) ∠A=90∘
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution
