ABCD is a rectangle with O as any point in its interior. If ar(ΔAOD)=3 cm2 and ar(ΔBOC)=6 cm2, then area of rectangle ABCD is
9 cm2
12 cm2
15 cm2
18 cm2
The correct Answer is:D
To find the area of rectangle ABCD given the areas of triangles AOD and BOC, we can follow these steps:
1. Identify the Given Areas:
- Area of triangle AOD = 3 cm²
- Area of triangle BOC = 6 cm²
2. Use the Property of Triangles and Parallelograms:
- According to the theorem, the area of a parallelogram formed by extending the sides of the triangles is equal to twice the area of the triangle that shares the same base and height.
- For triangle AOD, we can form a parallelogram ALMD (where L and M are points on AD and BC respectively).
- Thus, the area of parallelogram ALMD = 2 × area of triangle AOD = 2 × 3 cm² = 6 cm².
3. Calculate the Area of the Second Parallelogram:
- Similarly, for triangle BOC, we can form another parallelogram LMCB.
- The area of parallelogram LMCB = 2 × area of triangle BOC = 2 × 6 cm² = 12 cm².
4. Combine the Areas:
- The total area of rectangle ABCD is the sum of the areas of the two parallelograms:
Area of rectangle ABCD=Area of parallelogram ALMD+Area of parallelogram LMCB
=6 cm²+12 cm²=18 cm²
5. Final Answer:
- Therefore, the area of rectangle ABCD is 18 cm².
- Area of triangle AOD = 3 cm²
- Area of triangle BOC = 6 cm²
- According to the theorem, the area of a parallelogram formed by extending the sides of the triangles is equal to twice the area of the triangle that shares the same base and height.
- For triangle AOD, we can form a parallelogram ALMD (where L and M are points on AD and BC respectively).
- Thus, the area of parallelogram ALMD = 2 × area of triangle AOD = 2 × 3 cm² = 6 cm².
- Similarly, for triangle BOC, we can form another parallelogram LMCB.
- The area of parallelogram LMCB = 2 × area of triangle BOC = 2 × 6 cm² = 12 cm².
- The total area of rectangle ABCD is the sum of the areas of the two parallelograms:
Area of rectangle ABCD=Area of parallelogram ALMD+Area of parallelogram LMCB
=6 cm²+12 cm²=18 cm²
- Therefore, the area of rectangle ABCD is 18 cm².
Topper's Solved these Questions
Similar Questions
Knowledge Check
Q is a point in the interior of a rectangle ABCD. If QA=3cm,QB=4cmandQC=5cm, then the length of QD (in cm) is
A3√2B5√2C√34D√41ABCD is a rectangle and M is a point on CD . AC and BM meet at X .

It is given that CM =3MD. Find
(i) area of ΔCXM : area of ΔAXB
(ii) area of ΔBXC : area of rectangle ABCDA(i) 9:16
(ii) 3:11B(i) 9:16
(ii) 3:14C(i) 16:9
(ii) 14:3D(i) 16:9
(ii) 11:3
ABCD is a rectangle. Let E be a point on
AB and F a point on CD such that DE is
parallel to BF.If AE=3 cm and if the area
of triangle BFC = 6 square cm.
Consider the following statements :
1. Area of rectangle ABCD can be of the
form pq2 square cm where p,q are
distinct primes.
2. Area of the figure EBFD is of the form
r2 square cm where r is rational but not an integer.
Which of the above statements is/are correct ?
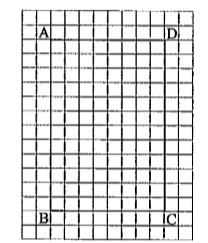
View SolutionThe given figure shows a rectangle ABCD of 12 cm length and 8 cm width, drawn on grid paper. Each square grid on the gird paper has a side of 1 cm and an area of 1 cm2.The area of rectangle ABCD is
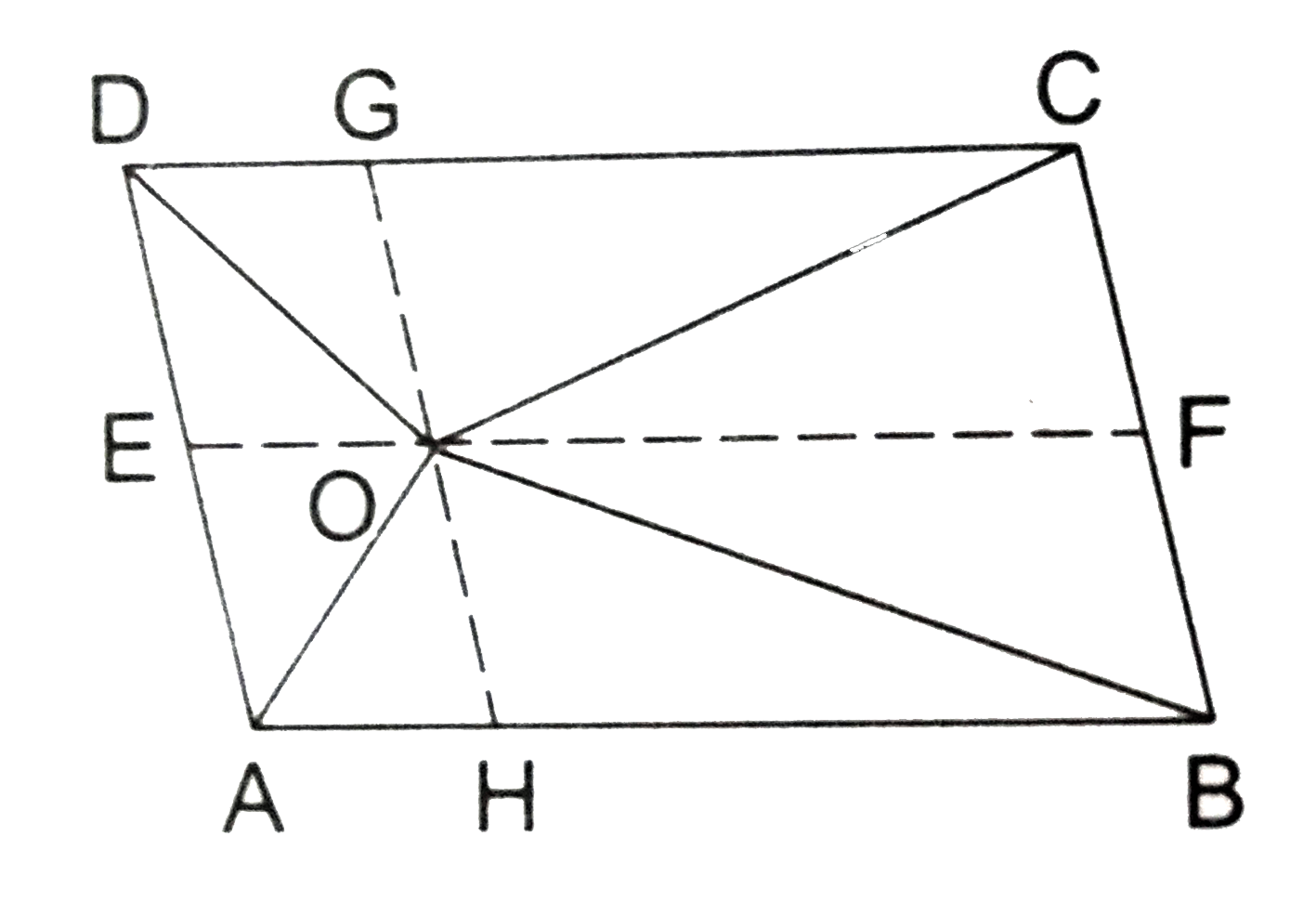
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionQ is a point interior of a rectangle ABCD . If QA=3cm,QB=4cm and QC=5cm,then length of QD is
View SolutionThe area of a rectangle is 650cm2 and its breadth is 13cm. The perimeter of the rectangle is
View Solution
