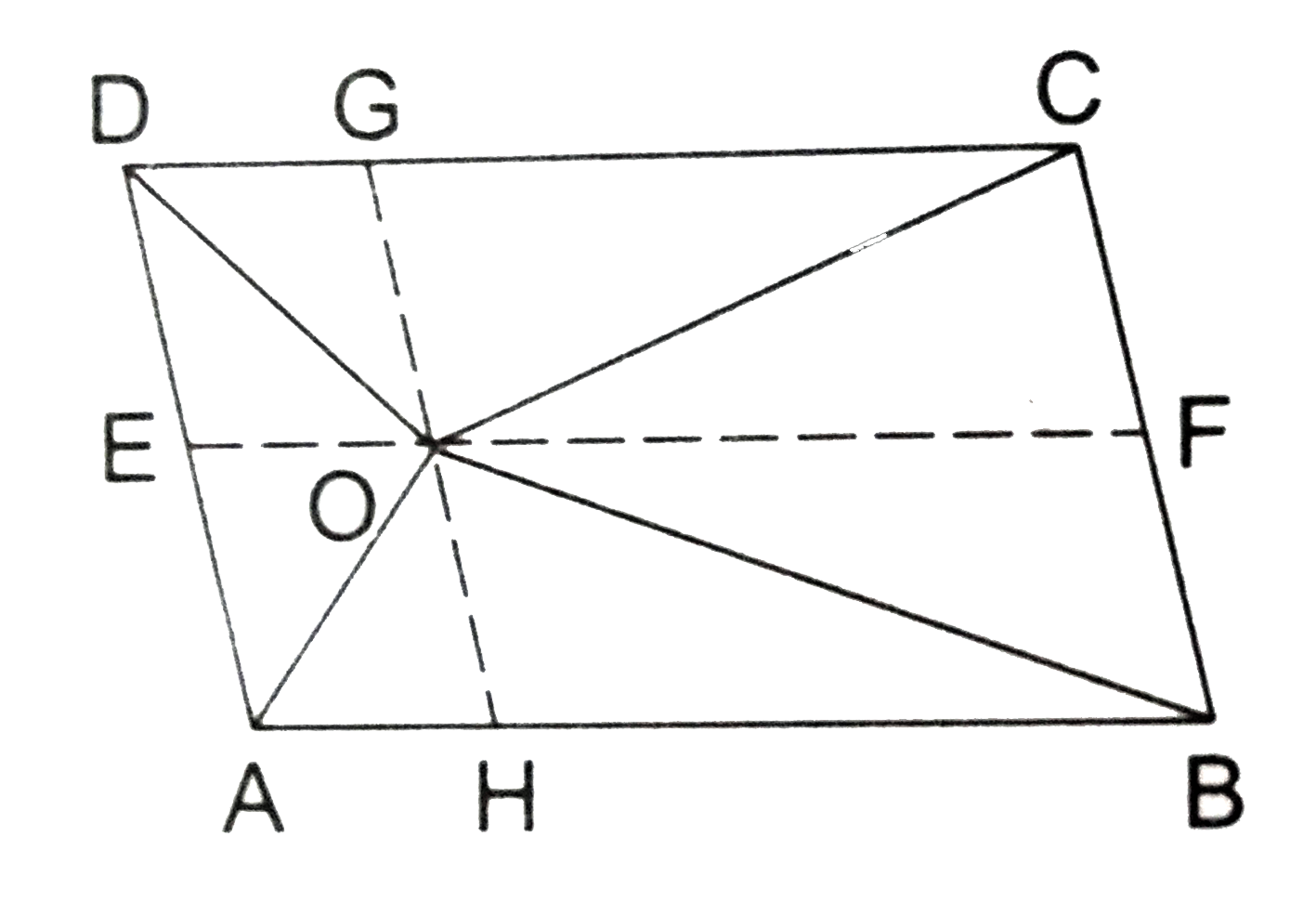
ABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
ABCD is a parallelogram
Diagonal AC and BD bisects each other.
Mid point of AC=Midpoint of BD
O is bisect BD in two part.
AO is themedian of∠ABD
Median divides the area of triangle ∠ABD in two equals parts.
area of∠AOD=areaof/_AOB
A=area of∠AOB
area(∠ADB)=4cm2.
Similar Questions
Knowledge Check
In the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
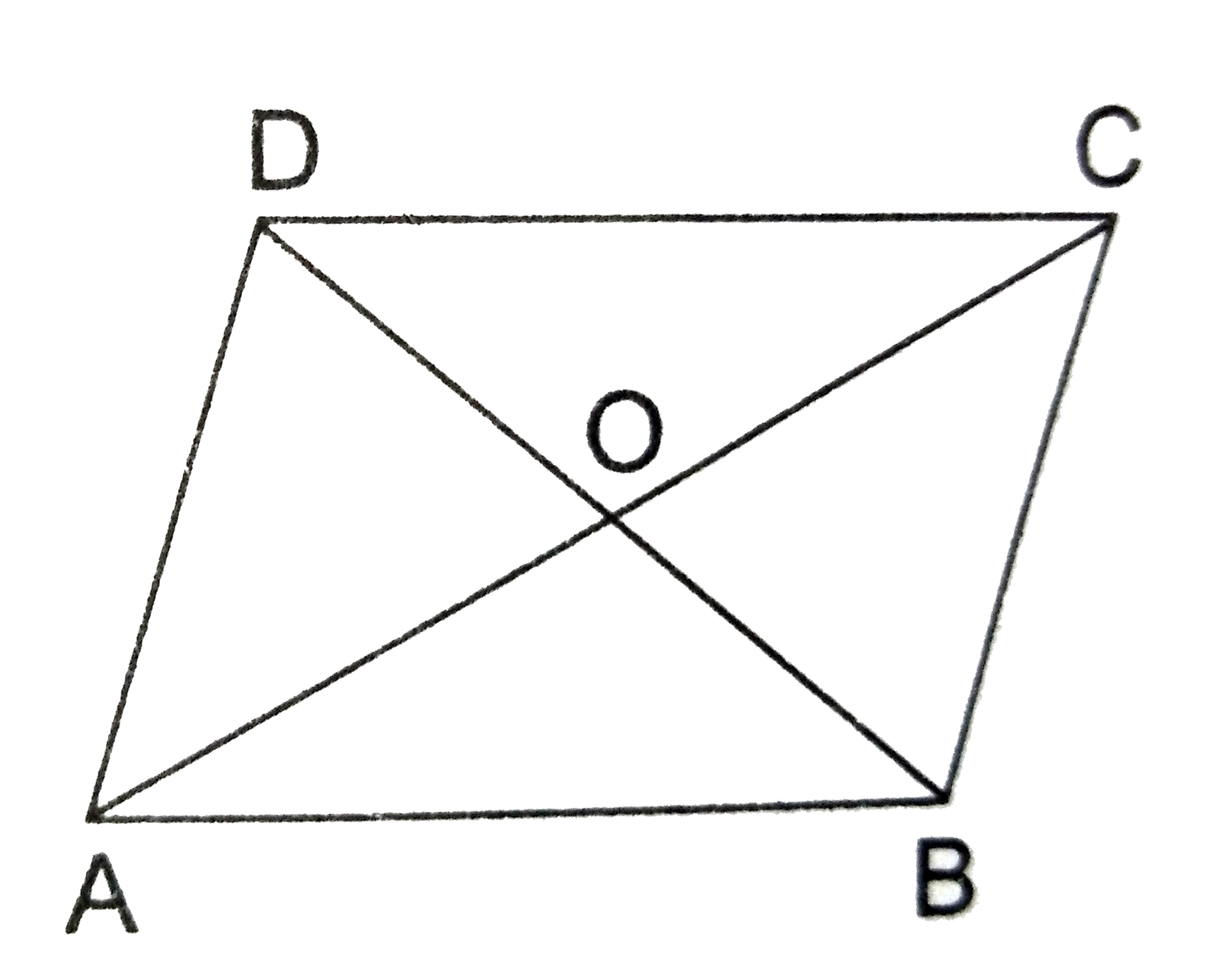 A26cm2B18.5cm2C39cm2D13cm2
A26cm2B18.5cm2C39cm2D13cm2Assertion (A) : In a trapezium ABCD, we have AB ||DC and the diagonals AC and BD intersect at O.
Then, ar(△AOD)=ar(△BOC).

Reason (R ) : Triangle on the same base between the same parallels are equal in area.ABoth Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).BBoth Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).CAssertion (A) is true and Reason (R ) is false.DAssertion (A) is false and Reason (R ) is true.
ABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionThe sides AD, BC of a trapezium. ABCD are parallel and the diagonals AC and BD meet at O. If the area of triangle AOB is 3 cm and the area of triangle BDC is 8 cm2, then what is the area of triangle AOD?
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
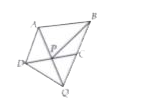
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO:OD=4:7, find
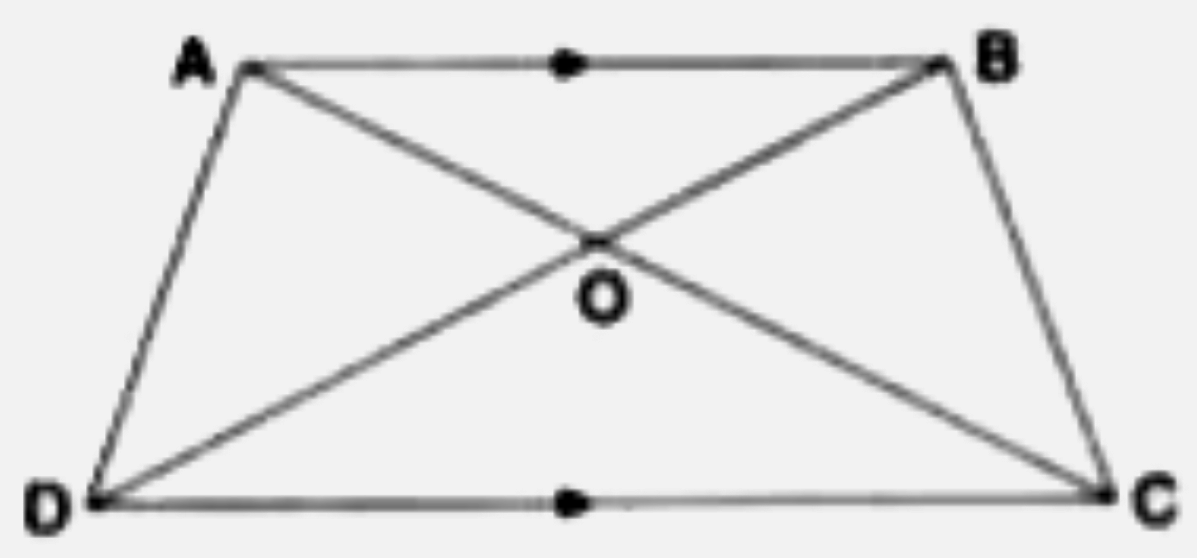
ΔAOD:ΔAOB
View SolutionE is any point on median AD of ∠ABC .If ar(ΔABE)=10cm2 then ar(ΔACE) is
View Solution