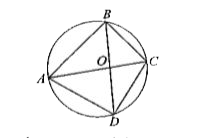
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
AC and BD are chords of circle.
anyline which is perpendicular and bisects the chord that line will pass through the centre.
BD=diameter and AC=diameter.
In
OC=OA
OB=OD
If alternate angle are equal AB||CD and AD||BC
ABCD is a cyclic quadrilateral
ABCD is a rectangle.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - CIRCLESEXERCISE - Exercise 10.12videos
CIRCLES
- BOOK - NCERTCHAPTER - CIRCLESEXERCISE - Solved Examples6videos
CIRCLES
- BOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.11videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.25videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
 ArectangleBsquareCtrapeziumDparallelogram
ArectangleBsquareCtrapeziumDparallelogram
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
View SolutionACandBD are chords of a circle that bisect each other. Prove that:AC and BD are diameter. ABCD is a rectangle
 View Solution
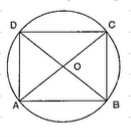
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
 View Solution
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
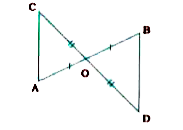
View SolutionTwo segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
View SolutionIn the given figure, prove that AC=BD.
 View Solution
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
View Solution

