Question

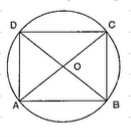
$ACandBD$
are chords of a circle which bisect each other. Prove that (i) $ACandBD$
are diameters (ii) $ABCD$
is a rectangle.

Explanation

(i) It is given that `AB` and `CD` are the two chords of a circle
Let the point of intersection be `O`.
Join AB,BC,CD and AD.

In triangles `AOB` and `COD`
,
`∠AOB=∠COD ` ...(Vertically opposite angles)

`OB=OD` ....(`O` is the mid-point of `BD`)
`OA=OC` ....(`O` is the mid-point of `AC`)
`△AOB≅△COD` ....`SAS` test of congruence
`∴AB=CD` ....c.s.c.t.
Similarly, we can prove
`△AOD≅△BOC,`
then we get

`AD=BC` ....c.s.c.t.
So, `□ABCD` is a parallelogram, since opposite sides are equal in length.
So, opposite angles are equal as well.
So, `∠A=∠C`
Also, for a cyclic quadrilateral opposite angles add up to `180^@`So,
`∠A+∠C=180^@`
`∠A+∠A=180^@`
`∠A=90^@`
So, `BD` is the diameter. Similarly, `AC` is also the diameter.
`(ii)` Since `AC` and `BD` are diameters,
`∴∠A=∠B=∠C=∠D=90^@` ...Angle inscribed in a semi circle is a right angle
Hence, parallelogram `ABCD` is a rectangle.