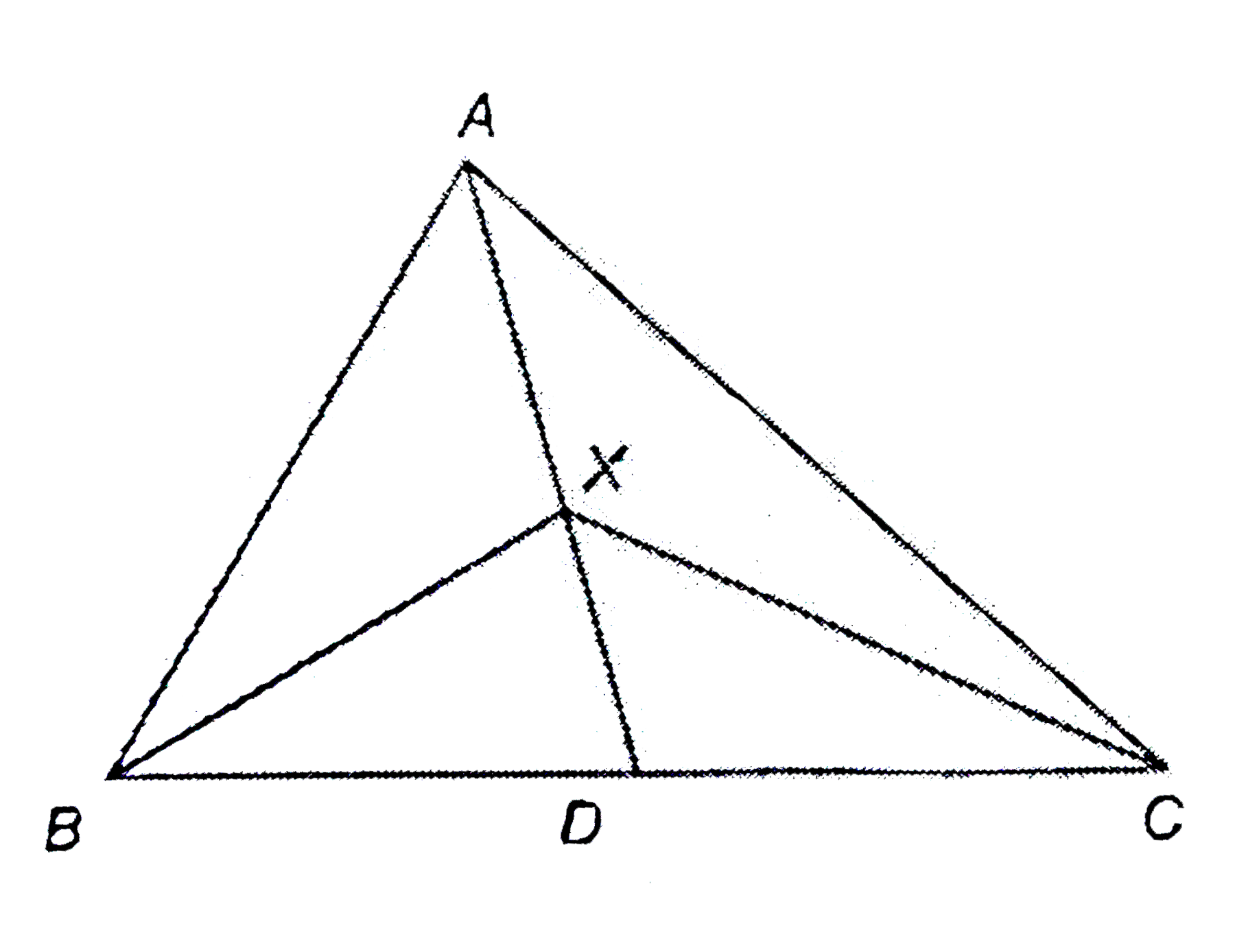
AD is the median of ABC and E is any point on AD. Which of the following statement is true ?
ar
ar
ar
ar
The correct Answer is:D
Step by step video, text & image solution for AD is the median of ABC and E is any point on AD. Which of the following statement is true ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PART-A (Fill in blanks :)18videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST3videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
If AD, BE and CF are medians of ΔABC, then which one of the following statements is correct ?
A(AD+BE+CF)<AB+BC+CABAD+BE+CF>AB+BC+CACAD+BE+CF=AB+BC+CADAD+BE+CF=√2(AB+BC+CA) - Question 2 - Select One
ABC is any triagnel inscribed in the circle x2+y2=r2 such that A is fixed point . If the external and internal bisectors of ∠A intersect the circle at D and E, respectively, then which of the following statements is true ΔADE ?
AIts centroid is a fixed point.BIts circumcentre is a fixed point.CIts orthocentre is a fixed point.Dnone of these - Question 3 - Select One
If any two irrational numbers are added, then which of the following statement is true?
AThe sum is always a rational numberBThe sum is always an irrational numberCThe sum may be rational or IrrationalDThe sum is always an integer
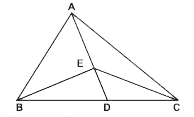
AD is one of the medians of a ABC..X is any point on AD . Show that ar(ABX)=ar(ACX)
View SolutionIn ΔABC, the median AD, BE and CF at G. then which of the following is correct?
View SolutionIf any two irrational numbers are added, then which of the following statement is true?
View SolutionIn ΔABC, the median AD, BE and CF at G. then which of the following is correct?
View SolutionIn a triangle ABC, D is a point on BC, such that any point on AD is equidistant from points B and C. Which of the following is necessarly true?
View Solution