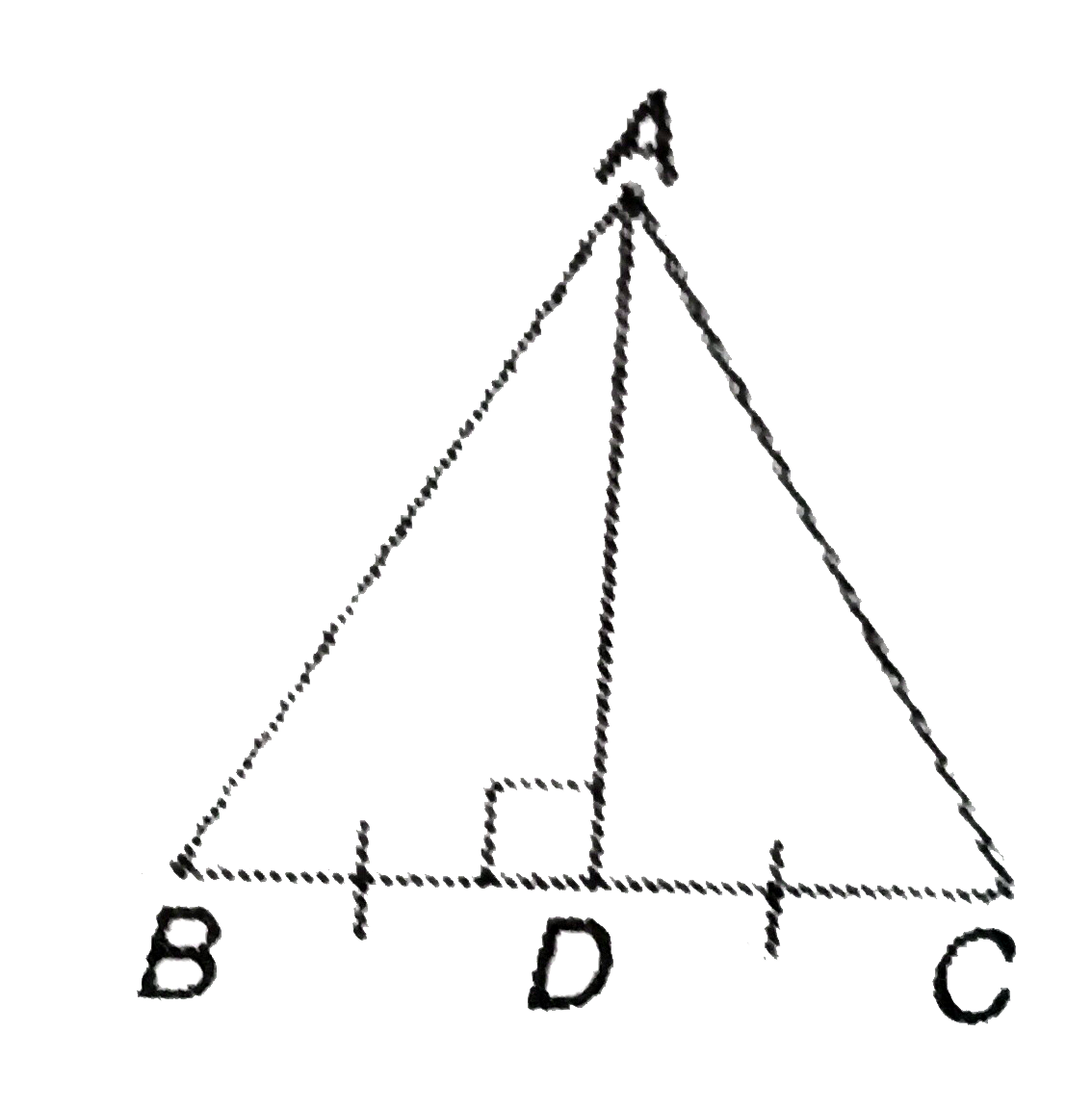
In a triangle ABC, D is a point on BC, such that any point on AD is equidistant from points B and C. Which of the following is necessarly true?
A
AB = BC
B
BC = AC
C
AC = AB
D
AB = BC = AC
Video Solution
Text Solution
The correct Answer is:C
Given, any point on AD is equidistant from B and C.
∴¯¯¯¯¯¯AD is the perpendicular bisector of ¯¯¯¯¯¯BC.
By SAS congruence property,
ΔADB=ΔADC
By CPCT, AB = AC.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOCUSEXERCISE - level 215videos
LOCUS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 310videos
LINEAR EQUATIONS AND INEQUATIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOGARITHMSEXERCISE - Level 3 MCQ15videos
LOGARITHMS
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABC is an equilateral triangle and D is a point on BC such that AD⊥BC, then
AAB:BD=1:1BAB:BD=1:2CAB:BD=2:1DAB:BD=3:2 - Question 2 - Select One
AD is the median of ABC and E is any point on AD. Which of the following statement is true ?
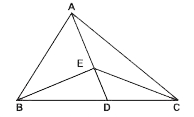 Aar (ΔABD)> ar (ΔACD)Bar (ΔABD)< ar (ΔACD)Car (ΔABE)= ar (ΔCED)Dar (ΔABE)= ar (ΔACE)
Aar (ΔABD)> ar (ΔACD)Bar (ΔABD)< ar (ΔACD)Car (ΔABE)= ar (ΔCED)Dar (ΔABE)= ar (ΔACE) - Question 3 - Select One
In a triangle ABC, D is a point on BC such that AD is the internal bisector of ∠A. Let ∠B=2∠C and CD = AB. Then ∠A is
A18∘B36∘C54∘D72∘
In a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View SolutionFind the locus of the point which is equidistant from the sides AB and AC of triangle ABC.
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.
 View Solution
View SolutionIn a △ABC,AC=BC, Point D lies on BC such that CD=AD=AB. Find ∠ACB.
View SolutionIn a ΔABC,D is a point on BC. AB is the hypotenus of then which relation is correct .
View Solution

