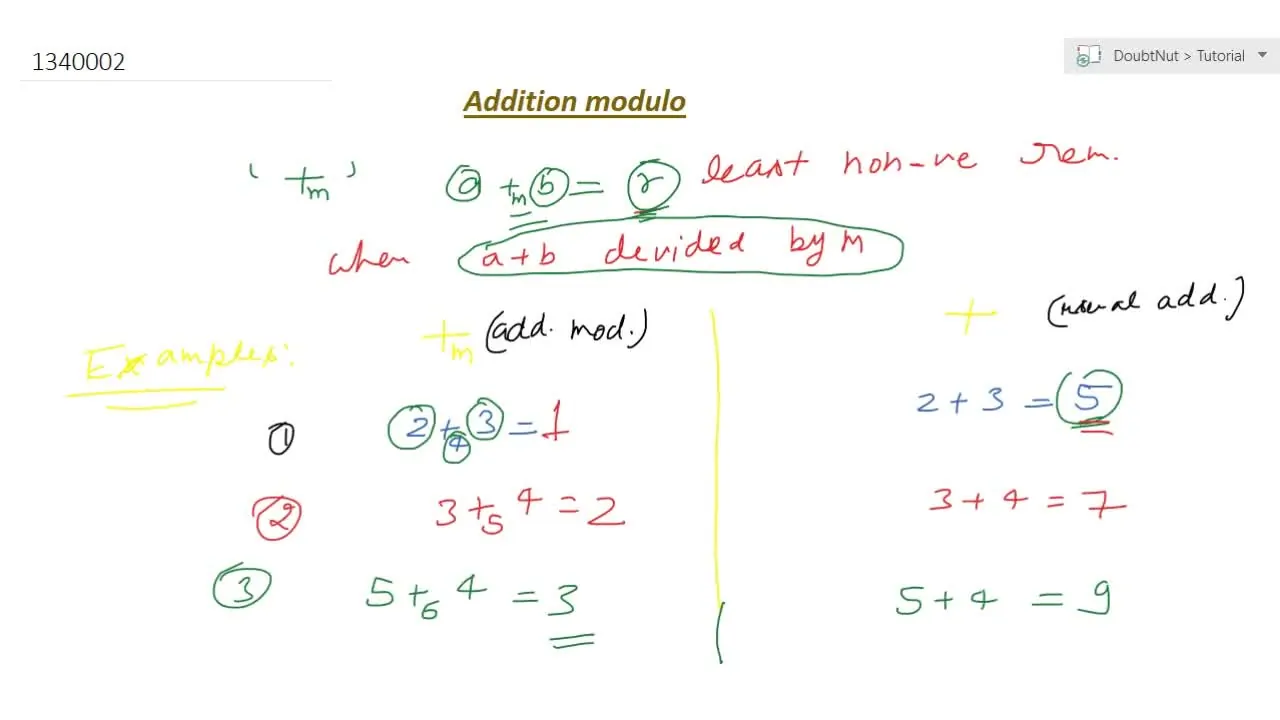
Addition Modulo
What is Addition Modulo?
Here, we will learn about the addition property of modular arithmetic:
(A + B) mod C = (A mod C + B mod C) mod C
Example:
Let A=14, B=17, C=5
Let's verify: (A + B) mod C = (A mod C + B mod C) mod C
LHS = Left Hand Side of the Equation
RHS = Right Hand Side of the Equation
LHS = (A + B) mod C
LHS = (14 + 17) mod 5
LHS = 31 mod 5
LHS = 1
RHS = (A mod C + B mod C) mod C
RHS = (14 mod 5 + 17 mod 5) mod 5
RHS = (4 + 2) mod 5
RHS = 1
LHS = RHS = 1
Intuition Behind Modular Addition
Observe the figure below. If we want to calculate 12+9 mod 7 we can easily go around the modular circle for a sequence of 12+9 steps clockwise (as shown in the bottom left circle).
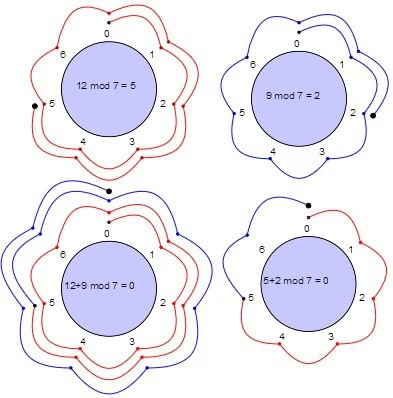
We can take a shortcut by observing that every 7 steps we end up in the same position on the modular circle. These complete loops around the modular circle don’t contribute to our final position. We ignore these complete loops around the circle by calculating each number mod 7 (as shown in the two upper modular circles). This will give us the number of clockwise steps, relative to 0, that contributed to each of their final positions around the modular circle.
Now, we only have to go around the circle clockwise the total of the number of steps that contributed to each of numbers final position (as shown in the bottom right modular circle). This method applies, in general, to any two integers and any modular circle.
Proof for Modular Addition
We will prove that (A + B) mod C = (A mod C + B mod C) mod C
We must show that LHS=RHS
From the quotient remainder theorem we can write A and B as:
A = C * Q1 + R1 where 0 ≤ R1 < C and Q1 is some integer. A mod C = R1
B = C * Q2 + R2 where 0 ≤ R2 < C and Q2 is some integer. B mod C = R2
(A + B) = C * (Q1 + Q2) + R1+R2
LHS = (A + B) mod C
LHS = (C * (Q1 + Q2) + R1+ R2) mod C
We can eliminate the multiples of C when we take the mod C
LHS = (R1 + R2) mod C
RHS = (A mod C + B mod C) mod C
RHS = (R1 + R2) mod C
LHS=RHS= (R1 + R2) mod C
LHS = Left Hand Side of the Equation
RHS = Right Hand Side of the Equation
LHS = (14 + 17) mod 5
LHS = 31 mod 5
LHS = 1
RHS = (14 mod 5 + 17 mod 5) mod 5
RHS = (4 + 2) mod 5
RHS = 1

We must show that LHS=RHS
B = C * Q2 + R2 where 0 ≤ R2 < C and Q2 is some integer. B mod C = R2
(A + B) = C * (Q1 + Q2) + R1+R2
LHS = (C * (Q1 + Q2) + R1+ R2) mod C
We can eliminate the multiples of C when we take the mod C
LHS = (R1 + R2) mod C
RHS = (R1 + R2) mod C
Similar Questions
Multiplication modulo
View SolutionFind the inverse of 5 under multiplication modulo 11 on Z11 .
View SolutionWrite the inverse of 5 under multiplication modulo 11 on the set {1, 2, ....., 10}.
View SolutionWrite the composition table for the binary operation multiplication modulo 10 (×10) on the set S={2, 4, 6, 8} .
View SolutionWrite the composition table for the binary operation multiplication modulo 10 (×10) defined on the set S={1, 3, 7, 9} .
View SolutionConstruct Caley's table for the set {0,1,2,3,4} under multiplication modulo 6.
View SolutionWrite the composition table for the binary operation ×5 (multiplication modulo 5) on the set S={0, 1, 2, 3, 4} .
View SolutionAngle Between Two Vectors|Questions|Laws Of Addition Of Vectors|Triangle Law Of Vector Addition|Polygon Law Of Vector Addition|Parallelogram Law Of Vector Addition
View SolutionAddition of bromine to trans-2-butene yields meso-2,3-dibromobutane.
Bromine addition is an electrophilic addition.View SolutionRecap|Properties Of Addition And Subtraction |Additive Identity|OMR|Summary
View Solution