α,β,γandδ are angles in I,II,II and IV quadrants, respectively and none of them is an integral multiple of π/2. They form an increasing arithmetic progression.
Which of the following does not hold?
sin(β+γ)=sin(α+δ)
sin(β−γ)=sin(α−δ)
tan2(α+β)=tan(β+δ)
cos(α+γ)=cos2β
The correct Answer is:B
To solve the problem, we need to analyze the angles α, β, γ, and δ which are in the first, second, third, and fourth quadrants respectively, and form an increasing arithmetic progression (AP). We are given that α=70∘.
1. Identify the Quadrants and Ranges:
- α is in the first quadrant: 0<α<90∘
- β is in the second quadrant: 90∘<β<180∘
- γ is in the third quadrant: 180∘<γ<270∘
- δ is in the fourth quadrant: 270∘<δ<360∘
2. Set Up the Arithmetic Progression:
Since α, β, γ, and δ are in an increasing AP, we can express them as:
- β=α+d
- γ=α+2d
- δ=α+3d
where d is the common difference.
3. Substituting the Known Value:
Given α=70∘:
- β=70∘+d
- γ=70∘+2d
- δ=70∘+3d
4. Determine the Range for Each Angle:
- For β (in the second quadrant):
90∘<70∘+d<180∘⟹20∘<d<110∘
- For γ (in the third quadrant):
180∘<70∘+2d<270∘⟹55∘<d<100∘
- For δ (in the fourth quadrant):
270∘<70∘+3d<360∘⟹66.67∘<d<96.67∘
5. Combine the Ranges for d:
From the inequalities derived:
- From β: 20∘<d<110∘
- From γ: 55∘<d<100∘
- From δ: 66.67∘<d<96.67∘
The effective range for d is:
66.67∘<d<96.67∘
6. Evaluate the Sine Functions:
We need to check which of the given options does not hold. The sine functions for the angles can be evaluated as follows:
- sin(β+γ)
- sin(α+d)
- sin(δ)
Using the sine addition formula:
sin(β+γ)=sin((α+d)+(α+2d))=sin(2α+3d)
7. Conclusion:
After evaluating the sine functions and their relationships, we find that the statement sin(β+γ)=sin(α+d) does not hold true based on the established ranges and properties of the sine function in different quadrants.
Final Answer:
The option that does not hold is B.
- α is in the first quadrant: 0<α<90∘
- β is in the second quadrant: 90∘<β<180∘
- γ is in the third quadrant: 180∘<γ<270∘
- δ is in the fourth quadrant: 270∘<δ<360∘
Since α, β, γ, and δ are in an increasing AP, we can express them as:
- β=α+d
- γ=α+2d
- δ=α+3d
where d is the common difference.
Given α=70∘:
- β=70∘+d
- γ=70∘+2d
- δ=70∘+3d
- For β (in the second quadrant):
90∘<70∘+d<180∘⟹20∘<d<110∘
- For γ (in the third quadrant):
180∘<70∘+2d<270∘⟹55∘<d<100∘
- For δ (in the fourth quadrant):
270∘<70∘+3d<360∘⟹66.67∘<d<96.67∘
From the inequalities derived:
- From β: 20∘<d<110∘
- From γ: 55∘<d<100∘
- From δ: 66.67∘<d<96.67∘
66.67∘<d<96.67∘
We need to check which of the given options does not hold. The sine functions for the angles can be evaluated as follows:
- sin(β+γ)
- sin(α+d)
- sin(δ)
sin(β+γ)=sin((α+d)+(α+2d))=sin(2α+3d)
After evaluating the sine functions and their relationships, we find that the statement sin(β+γ)=sin(α+d) does not hold true based on the established ranges and properties of the sine function in different quadrants.
The option that does not hold is B.
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Matrix Match Type
3 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Numerical Value Type
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Correct Answers Type
17 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
α,β,γandδ are angles in I,II,II and IV quadrants, respectively and none of them is an integral multiple of π/2. They form an increasing arithmetic progression.
Which of the following holds?
View Solutionα,β,γandδ are angles in I,II,II and IV quadrants, respectively and none of them is an integral multiple of π/2. They form an increasing arithmetic progression.
if α+β+γ+δ=θandα70∘, then
View Solution
Knowledge Check
Line l in the xy-plane contains points from each of Quadrants II, III, and IV, but no points from Quadrant I. Which of the following must be true?
AThe slope of line l is undefined.BThe slope of line l is zero.CThe slope of line l is positive.DThe slope of line l is negative.
In a arithmetic progression whose first term is α and common difference is β,α,β≠0 the ratio r of the sum of the first n terms to the sum of n terms succeending them, does not depend on n. Then which of the following is /are correct ?
View SolutionIf α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in column-I to their values in column-II:
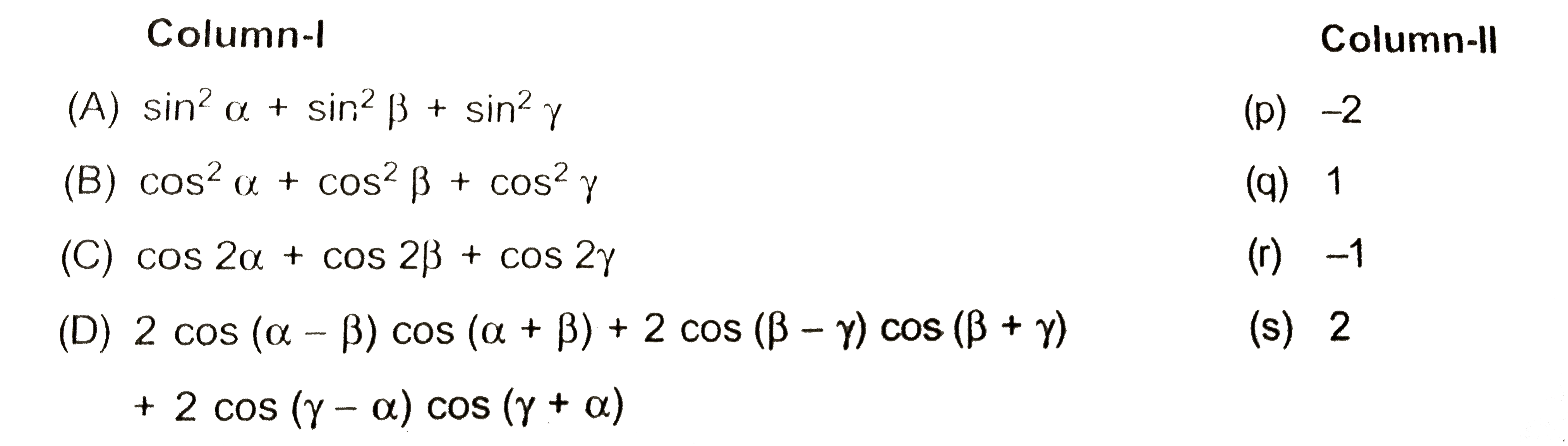
View SolutionConsider angles α=(2n+12)π±A and β=mπ+(−1)m(π2−A) where n, m ∈ I. Which of the following is not true ?
View SolutionFind the intervals in which f(x) = sin 3x, x∈[0,π2] is (i) increasing, (ii) decreasing.
View SolutionThe frquencies of Kα,Kβ and Lα X-rays of a materail are γ1,γ2andγ3 respectively. Which of the following relation holds good?
View SolutionFind the intervals in which the following functions are:
(i) increasing
.(ii)decreasing f(x)=2x2−6x
View SolutionThe vector →a=αˆi+2ˆj+βˆk lies in the plane of the vectors →b=ˆi+ˆj and →c=ˆj+ˆk and bisects the angle between →b and →c . Then which one of the following gives possible values of α and β ? (1) α=2,β=2 (2) α=1,β=2 (3) α=2,β=1 (4) α=1,β=1
View Solution
