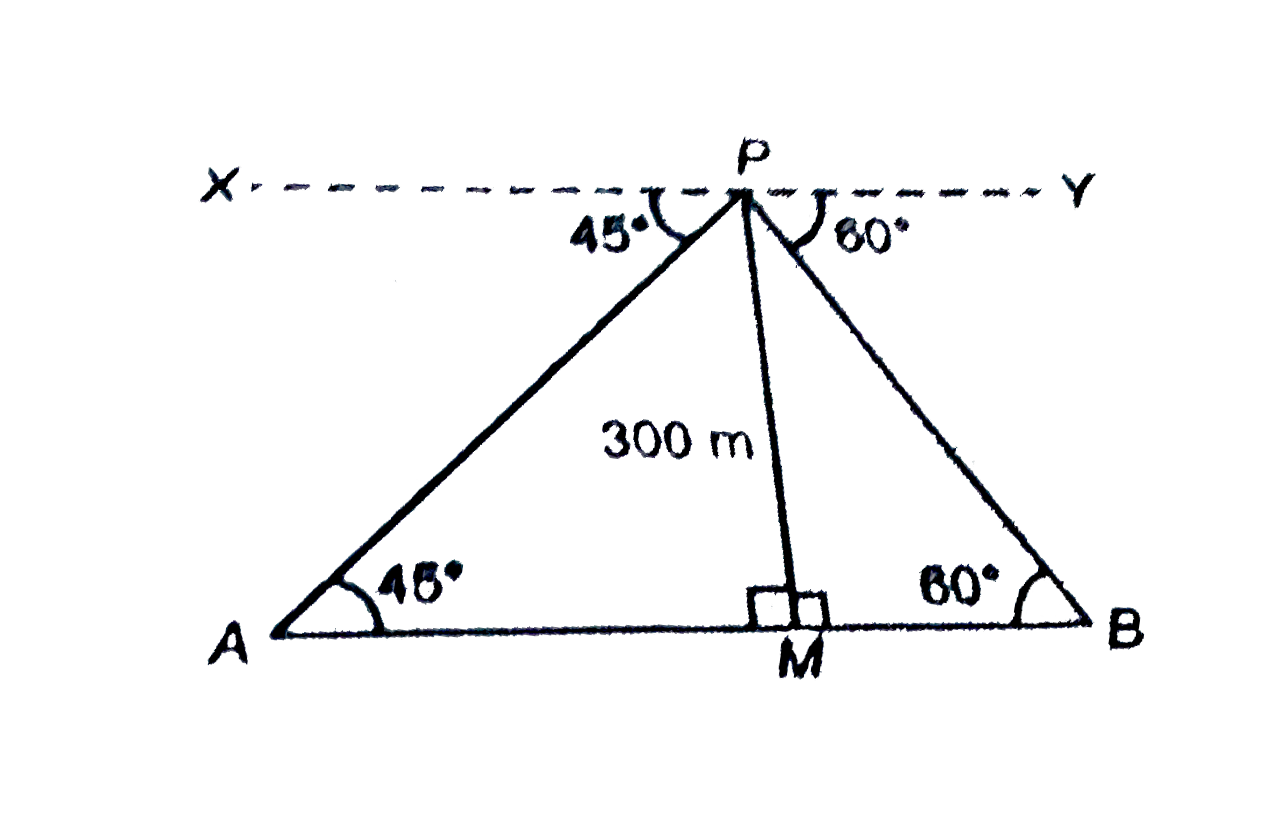
An aeroplane id flying at a height of 300 m above the ground. Fying at this height , theangles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45∘ and 60∘ respectively. Find the width of the river.[use √3=1.732]
let an aeroplane P is flying at a height of 300 m above the ground
∴PM=300m
Depression angles are ∠XPA=45∘ and ∠YPB=60∘. ∴∠PAM=45∘ and ∠PBM=60∘ (alternate angles)
Now, in right ΔPMA,
tan45∘=PMAM⇒1=300AM⇒AM=300m...(1)
In right ΔPMB,
tan60∘=PMMB⇒√3=300MB⇒MB=300√3=100√3...(2)
∴ WIdth of river =AM+MB
=(300+100√3)m=(300+100×1.732)m
=(300+173.2)m=473.20m
Hence, the width of the river -473.20 m
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBook:NAGEEN PRAKASHANChapter:SOME APPLICATIONS OF TRIGONOMETRYExercise:Exercise
Explore 32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBook:NAGEEN PRAKASHANChapter:SOME APPLICATIONS OF TRIGONOMETRYExercise:Revision Exercise (short Answer Questions)
Explore 5 Videos
- REAL NUMBERSBook:NAGEEN PRAKASHANChapter:REAL NUMBERSExercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
An aeroplane is flying at a height of 210 m. Flying at this height at some instant the angles of depression of two points in a line in opposite directions on both the banks of the river are 45∘ and 60∘. Find the width of the river. (Use √3=1.73)
View SolutionThe pilot of an aeroplane at an altitutde of 200 m observes the angle of depression of opposite points on the two banks of a river to be 45∘ and 60∘. Find the width of the river.
View Solution
Knowledge Check
An aeroplane flying at a height of 300 m above the ground passes vertically above another plane at an instant when the angles of elevation of two planes from the same point on the ground are 60∘and45∘, respectively. What is the height of the lower plane from the ground?
A50 mB100√3mC100√3mD150(√3+1)mAn aeroplane flying at a height of 300 m above the ground passes vertically above another plane at an instant when the angles of elevation of two planes from the same point on the ground are 60∘and45∘, respectively. What is the height of the lower plane from the ground?
A100√3B100/√3C50D150(√3+1)
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 450and600. Find the width of the river.
View SolutionAn aeroplane at an altitude of 200 m observes the angles od depression of opposite points on the two banks of a river to be 45∘and60∘. Find the width of the river.

View SolutionAn aeroplane at an altitude of 200 m observes angles of depression of opposite points on the two banks of the river to be 45∘ and 60∘, find the width of the river.
View SolutionAn aeroplane flying at a height of 3000 m passes vertically above another aeroplane at an instant when the angles of elevation of the two planes from some point on the ground are 60∘ and 45∘ respectively. Then the vertical distance between the two planes is
View SolutionAn aeroplane flying at a height 300 metre above the ground passes vertically above another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 60∘ and 45∘ respectively. Then the height of the lower plane from the ground in metres is
View SolutionAn aeroplane flying at a height 300 metre above the ground passes vertically above another plane at an instant when the angles of elcvation of the two planes from the same point on the ground are 60∘ and 45∘ respectively. Then the height of the lower plane from the ground (in metres) is
View Solution