An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
To find the maximum number of columns in which the army contingent of 616 members and the army band of 32 members can march, we need to determine the highest common factor (HCF) of the two numbers. Here’s how we can solve it step by step:
Step 1: Identify the two numbers
We have two groups:
- Army contingent: 616 members
- Army band: 32 members
Step 2: Use the HCF to find the maximum number of columns
To find the maximum number of columns, we need to calculate the HCF of 616 and 32.
Step 3: Apply the Division Method to find HCF
1. Divide the larger number (616) by the smaller number (32).
2. Calculate the quotient and the remainder.
616÷32=19(quotient)
Remainder=616−(32×19)=616−608=8
So we can write:
616=32×19+8
3. Now, take the divisor (32) and divide it by the remainder (8).
32÷8=4(quotient)
Remainder=32−(8×4)=32−32=0
So we can write:
32=8×4+0
Step 4: Conclude the HCF
Since the remainder is now 0, the last non-zero remainder is the HCF. Therefore, the HCF of 616 and 32 is 8.
Final Answer
The maximum number of columns in which the army contingent and the army band can march is 8.
---
We have two groups:
- Army contingent: 616 members
- Army band: 32 members
To find the maximum number of columns, we need to calculate the HCF of 616 and 32.
1. Divide the larger number (616) by the smaller number (32).
2. Calculate the quotient and the remainder.
Remainder=616−(32×19)=616−608=8
616=32×19+8
Remainder=32−(8×4)=32−32=0
32=8×4+0
Since the remainder is now 0, the last non-zero remainder is the HCF. Therefore, the HCF of 616 and 32 is 8.
The maximum number of columns in which the army contingent and the army band can march is 8.
Topper's Solved these Questions
Similar Questions
Any contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
View SolutionCadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (Use n for the number of rows.)
View Solution
Knowledge Check
- Question 1 - Select One
There are 45 Musicians in an orchestra , and all play two instruments . Of these musicians , 36 play the piano , and 22 play the violin . What is the maximum possible number of orchestra members who play both the piano and the violin ?
A9B13C22D23
Read the bar graph given in Figure and answer the following questions: What is the information given by the bar graph? What is the number of families having 6 members? How many member per family are there in the maximum number of families? Also tell the number of such families. What are the number of members per family for which the number of families are equal? Also, tell the number of such families?
View SolutionA group of 2n students consisting of n boys and n girls are to be arranged in a row such that adjacent members are of opposite sex. The number of ways in which this can be done is
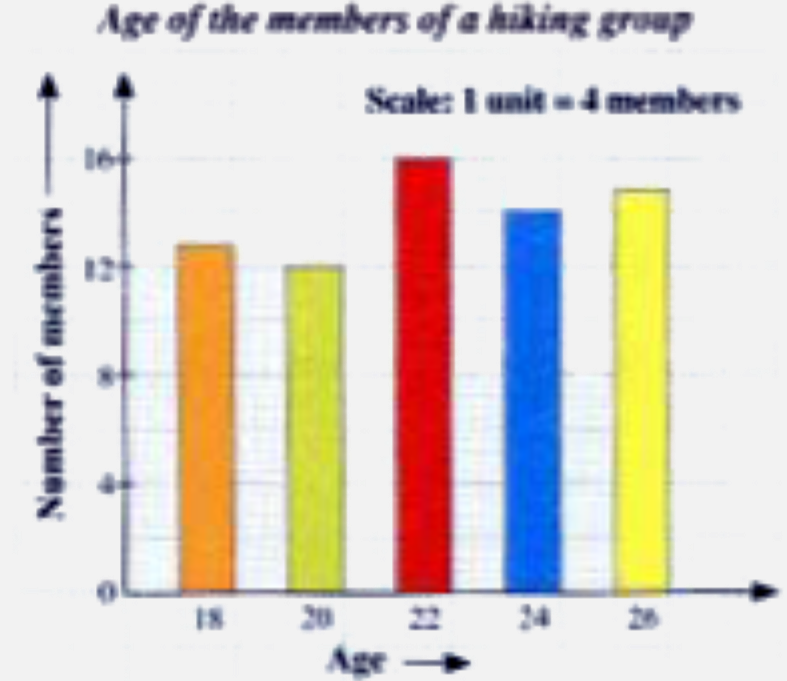
View SolutionThe given graph represents the age and number of members of a hiking group who are planning an excursion. Study the graph and answer the following question.
Which age group has the maximum members in the hiking gruoup?
 View Solution
View SolutionWhich of the following statements related to the modern periodic table is incorrect?
a.The p-block has 6 columns, because a maximum of 6 electrons can occupy all the orbitals in a p-shell.
b.The d-blocks has 8 columns, because a maximum of 8 electrons can occupy all the orbitals in a d-subshell.
c.Each block contains a number of columns equal to the number of electrons that can occupy that subshell.
d.The block indicates value of azimuthal quantum number (l) for the last subshell that received electrons in building up the electronic configuration.View SolutionFind the number of ways in which two small squares can be selected on the normal chessboard if they are not in same row or same column.
View SolutionIn a high school, a committee has to be formed from a group of 6 boys M1, M2, M3, M4, M5, M6 and 5 girls G1, G2, G3, G4, G5 . Let α1 be the total number of ways in which the committee can be formed such that the committee has 5 members, having exactly 3 boys and 2 girls. (ii) Let α2 be the total number of ways in which the committee can be formed such that the committee has at least 2 members, and having an equal number of boys and girls. (iii) Let α3 be the total number of ways in which the committee can be formed such that the committee has 5 members, at least 2 of them being girls. (iv) Let α4 be the total number of ways in which the committee can be formed such that the committee has 4 members, having at least 2 girls and such that both M1 and G1 are NOT in the committee together. LIST-I LIST-II P. The value of α1 is 1. 136 Q. The value of α2 is 2. 189 R. The value of α3 is 3. 192 S. The value of α4 is 4. 200 5. 381 6. 461 The correct option is: P→4; Q→6; R→2; S→1 (b) P→1; Q→4; R→2; S→3 (c) P→4; Q→6; R→5; S→2 (d) P→4; Q→2; R→3; S→1
View SolutionColumn I, Column II Number of straight lines joining any two of 10 points of which four points are collinear, p. 30 Maximum number of points of intersection of 10 straight lines in the plane, q. 60 Maximum number of points of intersection of six circles in the plane, r. 40 Maximum number of points of intersection of six parabolas, s. 45
View Solution

