An ellipse E has the equation x236+y232=1 and C and S are its centre and a focus the usual notation. A hyperbola H has a vertex at C, point S as its focus nearer to C and latus rectum of equal length to that of E. Show that H has the eccentricity 53 and find its equationSolution in Bengali
The correct Answer is:16x2−9y2+96x=0
Step by step video, text & image solution for An ellipse E has the equation (x^(2))/(36) + (y^(2))/(32) = 1 and C and S are its centre and a focus the usual notation. A hyperbola H has a vertex at C, point S as its focus nearer to C and latus rectum of equal length to that of E. Show that H has the eccentricity (5)/(3) and find its equation by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABook:CHHAYA PUBLICATIONChapter:HYPERBOLAExercise:SAMPLE QUESTIONS FOR COMPETITIVE EXAMS
Explore 12 Videos
- HYPERBOLABook:CHHAYA PUBLICATIONChapter:HYPERBOLAExercise:SHORT ANSWER TYPE QUESTIONS
Explore 37 Videos
- DIAGRAMMATIC REPRESENTATION OF DATABook:CHHAYA PUBLICATIONChapter:DIAGRAMMATIC REPRESENTATION OF DATAExercise:EXERCISE (Very short Answer Type Question)
Explore 7 Videos
- MATHEMATICAL INDUCTION Book:CHHAYA PUBLICATIONChapter:MATHEMATICAL INDUCTION Exercise:Sample Questions for Competitive Exams
Explore 20 Videos
Similar Questions
The equation px2+2qxy+ry2+2sx+2ty+u=0 (where p≠q≠r and p,q,r,s,t and u are constants ) represents-
View SolutionFind (i) the length of axes (ii) length of latus rectum (iii) coordianates of vertices (iv) eccentricity (v) coordinates of foci and (vi) equations of the directries of each of the following hyperbolas:
(a) 4x2−9Y2=36 (b) 9y2−25x2=225
View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
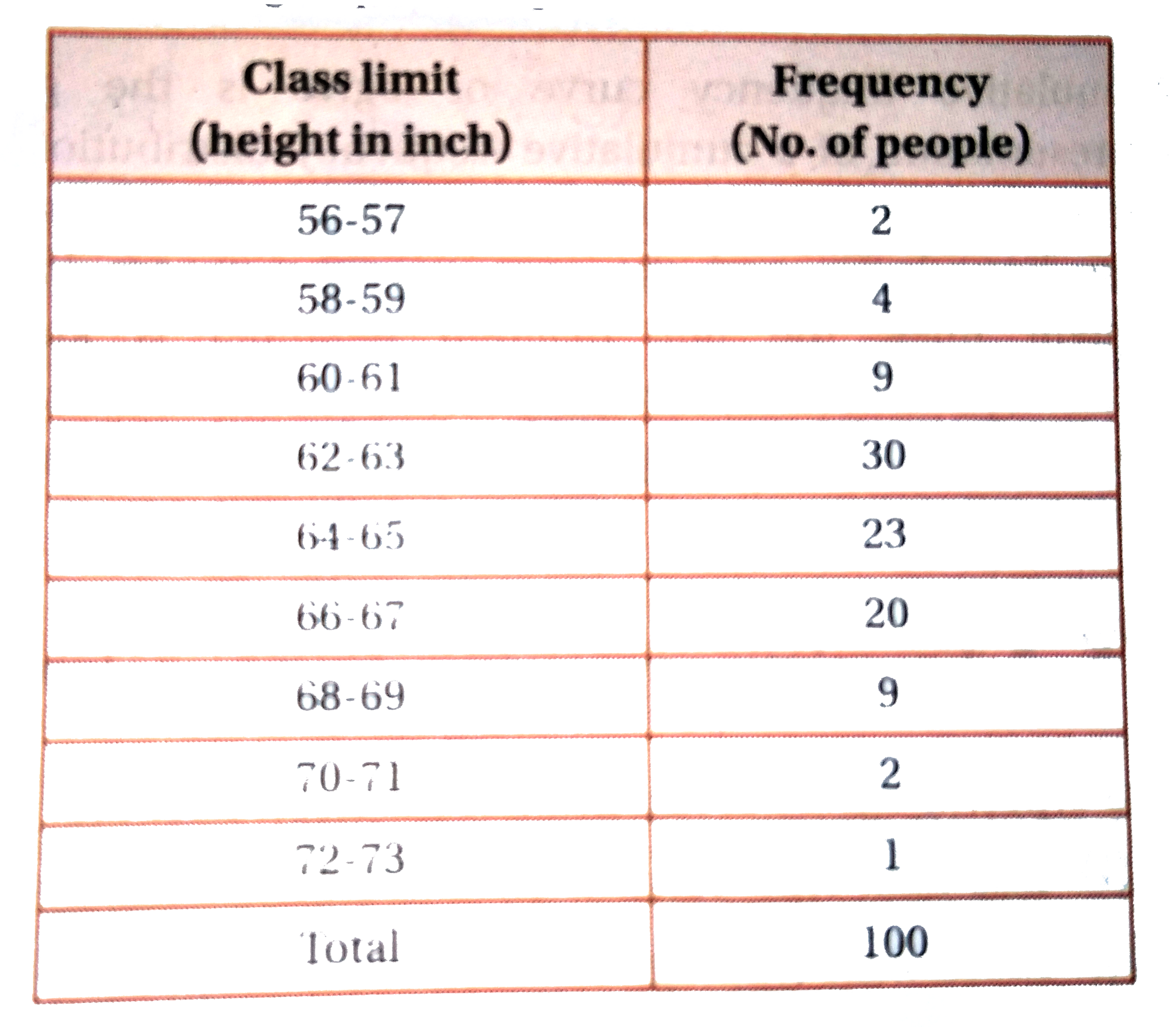 Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
View SolutionThe foci of the hyperbola are S(-3,-2), S' (5,6) If its e=2 then the equation of its directrix corresponding to focus S is :
View Solutiony2+2y−x+5=0 represents a parabola. Find its vertex, equation of axis, equation of latus rectum, coordinates of the focus, equation of the directrix, extremities of the latus rectum, and the length of the latus rectum.
View SolutionFind the value of λ if the equation (x−1)2+(y−2)2=λ(x+y+3)2 represents a parabola. Also, find its focus, the equation of its directrix, the equation of its axis, the coordinates of its vertex, the equation of its latus rectum, the length of the latus rectum, and the extremities of the latus rectum.
View SolutionFind the equation of the ellipse whose focus is S(-1,1), the corresponding directrix is x-y+3=0, and eccentricity is 1/2. Also find its center,the second focus,the equation of the second directrix,and the length of latus rectum.
View SolutionA parabola with vertex at origin has its focus at the center of x2+y2−10x+9=0 Find its directrix and latus rectum.
View SolutionIf the latus rectum of a hyperbola through one focus subtends 60∘ at the other focus then its eccentricity e=
View SolutionLet LL' be the latus rectum through the focus S of a hyperbola and A ' be the farther vertex of the conic .If ΔA' LL' is equilateral then its eccentricity e=
View SolutionThe eccentricity of an ellipse is 12 and its one focus is at S(3,2) , if the vertex nearer of S be A (5,4) , find the equation of the ellipse .
View SolutionIf the length of the latus rectum of an ellipse is 4 units and the distance between a focus and its nearest vertex on the major axis is 32 units, then its eccentricity is:
View Solutione is the eccentricity of the ellipse 4x2+9y2=36 and C is the centre and S is the focus and A is the vertex then CS:SA=
View SolutionAn ellipse has directrix x+y=-2 focus at (3,4) eccentricity =1//2, then length of latus rectum is
View Solution
