An ellipse is drawn with major and minor axis of length 10 and 8 respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is Solution in Bengali
The correct Answer is:2
Givemn ellipse
x225+y216=1
∴E2=1−1625ore=35
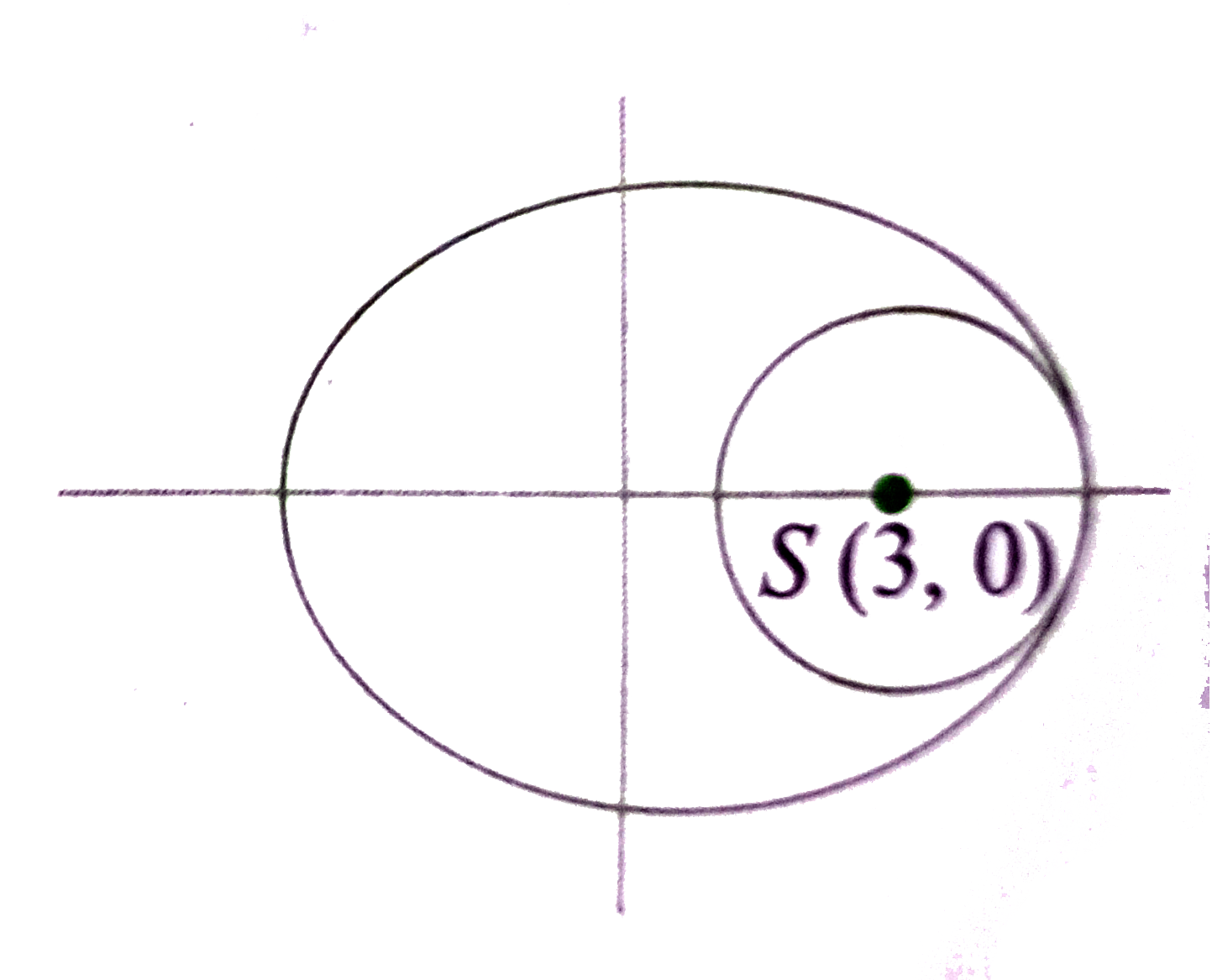
then foci are (±ae,0)≡(±3,0)
Now, the circle having center (3,0) is
(x−3)2+y2=r2
Eliminating y2 from (1) and (2), we get
16x2+25r2−25(x2−6x+9)=400
or −9x2+150x+25r2−625=0
since the circle touches the ellipse, the above equation, has equal roots. Hence D=0,i.e.,22500+36(25r2−625)=0, which is not possible
Then the circle will touche the ellipse at the end of the major axis, (5,0) Hence, the radius is 2
Similar Questions
If a circle is concentric with the ellipse, find the inclination of their common tangent to the major axis of the ellipse.
View SolutionAn ellipse is drawn with major and minor axis of length 10 and 8 respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is
View Solutionमाना दीर्घवृत्त की नाभियाँ (-1,0) तथा (3, 4) है तथा नाभि (3,4) से दीर्घवृत्त पर खींची गयी किसी स्पर्श रेखा के लम्ब के पाद के निर्देशांक (4,6) है।
दीर्घवृत्त के सहायक वृत्त का समीकरण होगा
View SolutionThe lengths of major and minor axis of an ellipse are 10 and 8 respectively and its major axis is along the Y-axis. The equation of the ellipse referred to its centre as origin is
View Solutionएक दीर्घवृत्त बनाया जाता है, जिसकी दीर्घ अक्ष तथा लघु अक्ष क्रमश:10 तथा 6 है। एक नाभि को केन्द्र मानकर एक वृत्त बनाया जाता है, जो दीर्घवृत्त को स्पर्श करता है तथा वृत्त का कोई भी भाग दीर्घवृत्त के बाहर नहीं है। वृत्तकी त्रिज्या है
View SolutionPoint 'O' is the centre of the ellipse with major axis AB & minor axis CD. Point F is one focus of the ellipse. If OF = 6 & the diameter of the inscribed circle of triangle OCF is 2, then find the product (AB).(CD)
View SolutionAn ellipse is drawn with major and minor axis of length 10 and 8 respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is (A) √3 (B) 2 (C) 2√2 (D) √5
View SolutionAn ellipse is drawn with major and minor axis of length 10 and 8 respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is
View Solution
