An ellipse is inscribed in a reactangle and the angle between the diagonals of the reactangle is tan−1(2√2), then find the ecentricity of the ellipse
The correct Answer is:1√2
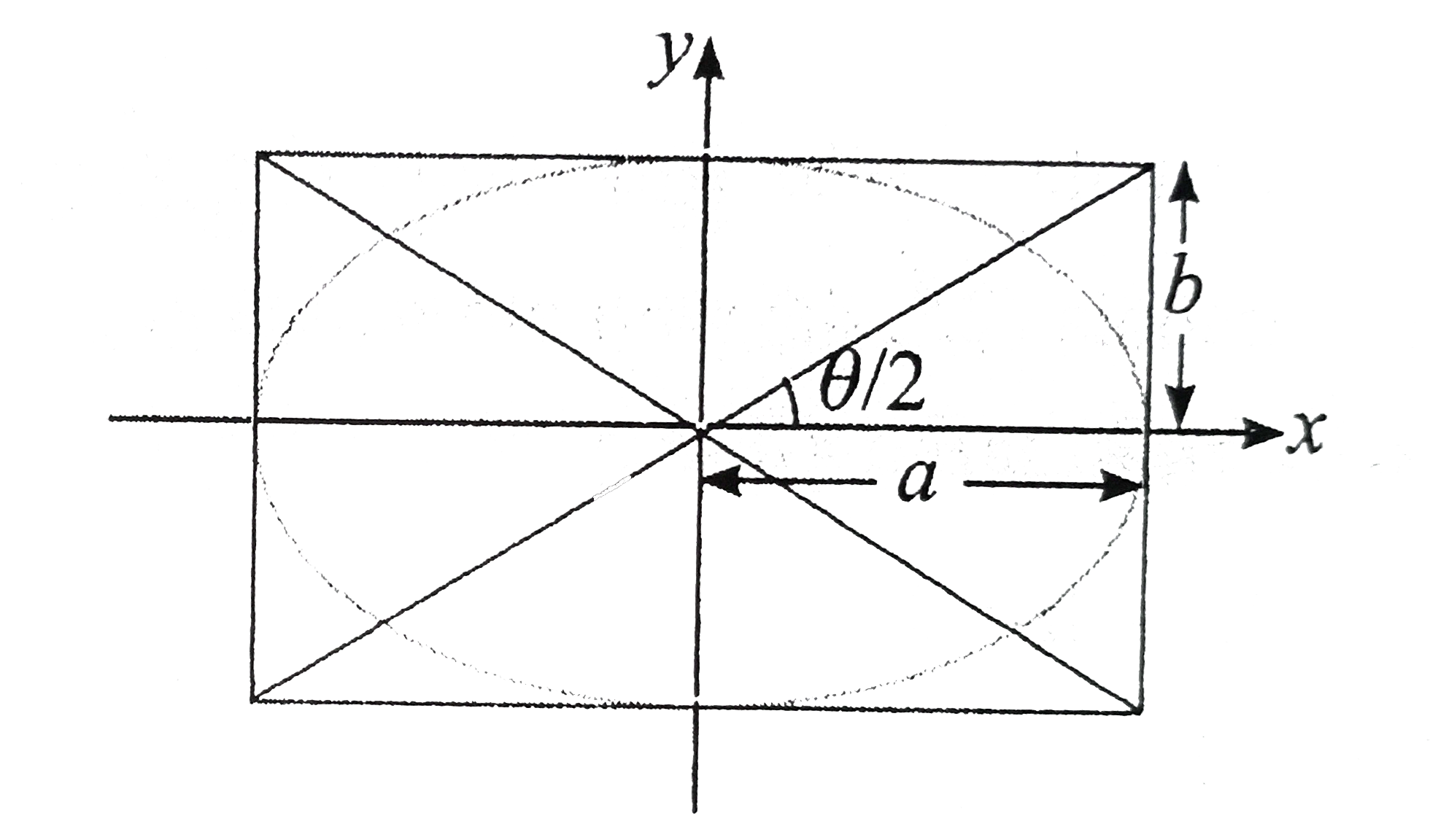
From the figure, we have
tan.θ2=ba⇒tan2.θ2=b2a2
⇒1−cosθ1+cosθ=b2a2
⇒1−131+13=b2a2⇒b2a2=12
∴e=√1−b2a2=1√2
Similar Questions
Knowledge Check
Ellipse x2+4y2=4 is inscribed in a rectangle aligned with co-ordinate axes . This rectangle itself is inscribed in another ellipse the passes ellipse that through (-4,0) . Then the equation of the ellipse is
Ax2+16y2=16Bx2+12y2=16C4x2+48y2=48D4x2+64y2=48
A reactangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle
View SolutionA reactangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle
View SolutionShow that for all real p the line 2px+y√1−p2=1 touches a fixed ellipse . Find the ecentricity of this ellipse.
View SolutionShow that for all real p the line 2px+y√1−p2=1 touches a fixed ellipse . Find the ecentricity of this ellipse.
View SolutionThe expresson are the areas of reactangle. Find the possible lengths and breadths of these reactangle.
x2−6x+8
View SolutionThe ratio of the area of triangle inscribed in ellipse x2a2+y2b2=1 to that of triangle formed by the corresponding points on the auxiliary circle is 0.5. Then, find the eccentricity of the ellipse. (A) 12 (B) √32 (C) 1√2 (D) 1√3
View SolutionThe expresson are the areas of reactangle. Find the possible lengths and breadths of these reactangle.
x2−3x+2
View Solution
