An ellipse is inscribed in a reactangle and the angle between the diagonals of the reactangle is tan−1(2√2), then find the ecentricity of the ellipse Solution in Tamil
The correct Answer is:1√2
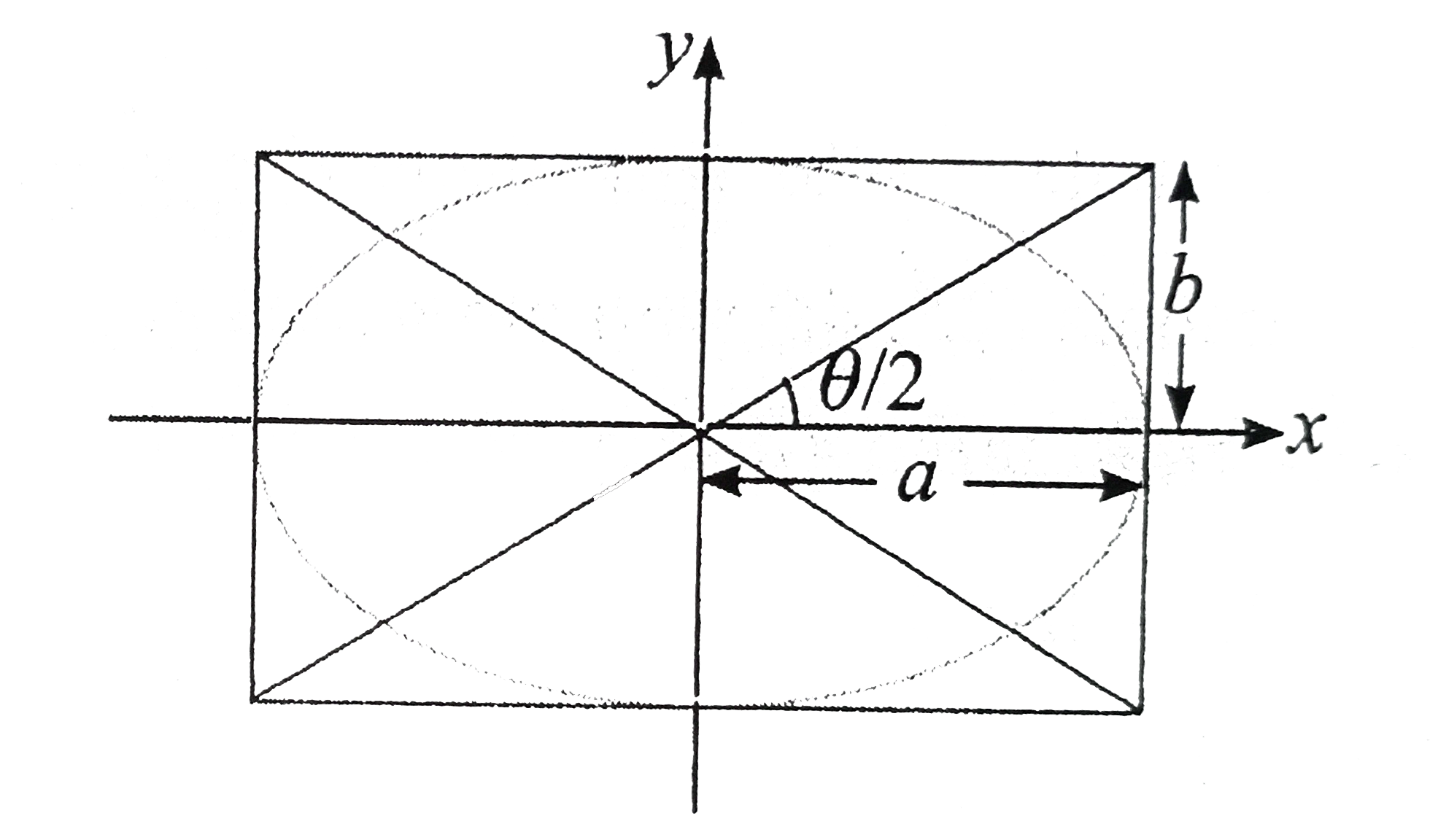
From the figure, we have
tan.θ2=ba⇒tan2.θ2=b2a2
⇒1−cosθ1+cosθ=b2a2
⇒1−131+13=b2a2⇒b2a2=12
∴e=√1−b2a2=1√2
Similar Questions
Maximum area of a reactangle which can be inscribed in a circle of a given radius R is
View SolutionThe area of a reactangle is x2+12xy+27y2 and its length is (x+9y). Find the breadth of the reactangle.
View SolutionThe expresson are the areas of reactangle. Find the possible lengths and breadths of these reactangle.
x2−6x+8
View SolutionThe expresson are the areas of reactangle. Find the possible lengths and breadths of these reactangle.
x2−3x+2
View SolutionThe expresson are the areas of reactangle. Find the possible lengths and breadths of these reactangle.
x2−7x+10
View SolutionThe expresson are the areas of reactangle. Find the possible length and breadth of these reactangle.
x2+19x−20
View SolutionThe expresson are the areas of reactangle. Find the possible lengths and breadths of these reactangle.
x2+9x+20
View SolutionFind the length a diagonal of a reactangle having sides 11 cm and 60cm.
View Solution
