An equilateral triangle is inscribed in the circle $x^{2} + y^{2} = a^{2}$ with one of the vertices at (a,0). What is the equation of the side opposite to this vertex ?

A

$2 x - a = 0$

B

$x + a = 0$

C

$2 x + a = 0$

D

$3 x - 2 a = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Since the equilateral is inscribed in the circle with centre at the origin, centroid lies on the origin.
So, $\frac{A O}{O D} = \frac{2}{1}$
and $O D = \frac{1}{2} A O = \frac{a}{2}$
So, other vertices of a triangle have coordinates,
$(- \frac{a}{2}, \frac{\sqrt{3 a}}{2})$ and $[- \frac{a}{2}, - \frac{\sqrt{3}}{2} a]$
$(- \frac{a}{2} \frac{\sqrt{3}}{2} a)$

$(- \frac{a}{2}, \frac{- \sqrt{3 a}}{2})$
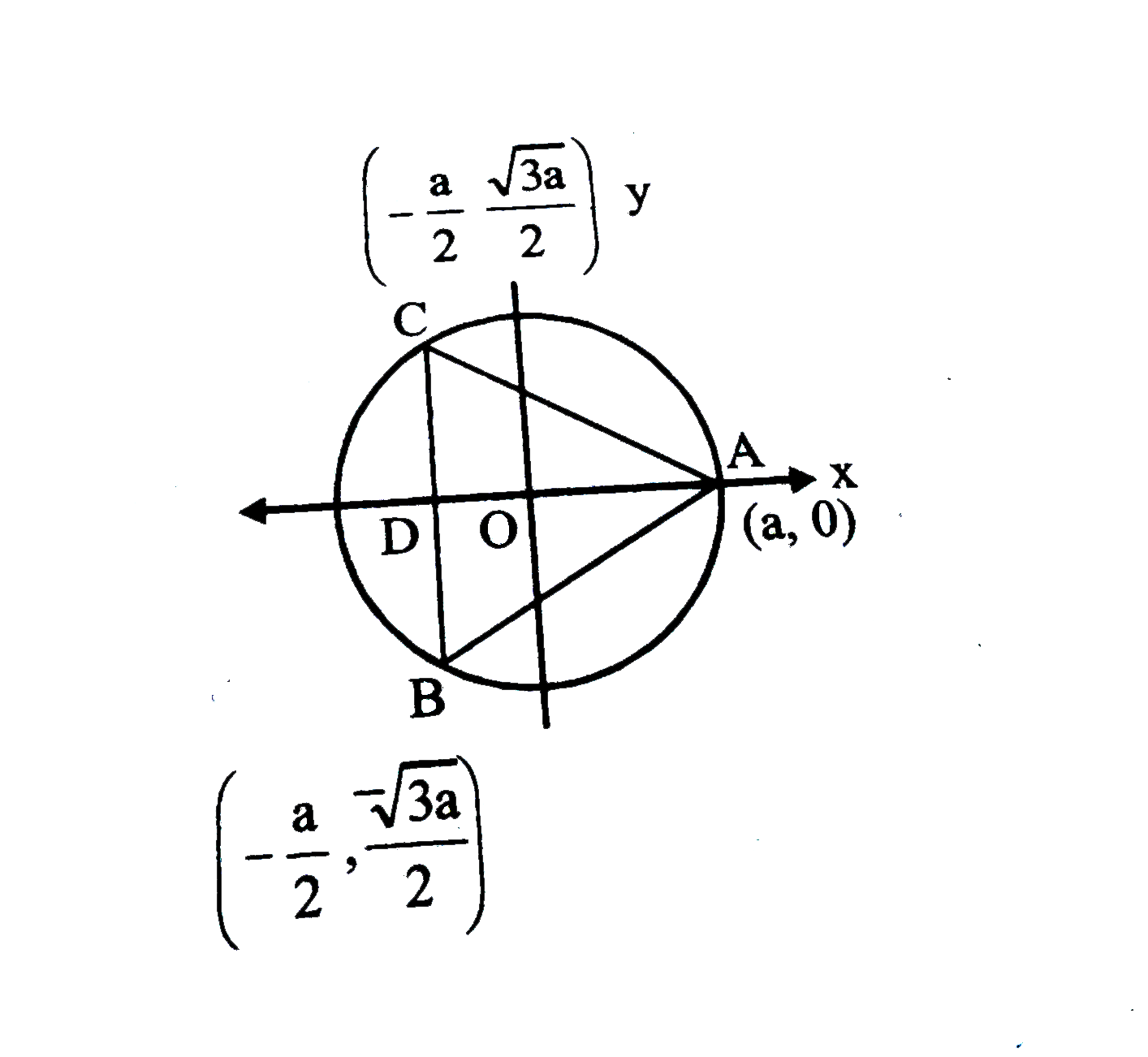
$∴$ Equation of line $B C$ is :
$x = - \frac{a}{2}$
$\Rightarrow 2 x + a = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Area of the equilateral triangle inscribed in the circle $x^{2} + y^{2} - 7 x 9 y + 5 = 0$ is
A $\frac{155}{8} \sqrt{3} s q u n i t s$
B $\frac{165}{8} \sqrt{3} s q u n i t s$
C $\frac{175}{8} \sqrt{3} s q u n i t s$
D $\frac{185}{8} \sqrt{3} s q u n i t s$
Question 2 - Select One
An equilateral triangle is inscribed in a circle of radius $6$ cm. Find its side.
A $6 \sqrt{3}$
B $\frac{6}{\sqrt{3}}$
C $8 \sqrt{3}$
D $2 \sqrt{3}$
Question 3 - Select One
An equilateral triangle is inscribed in the circle $x^{2} + y^{2} = 1$ which one vertex at the point $(1, 0) .$ Length of each side of the tringle is
A1
B $\sqrt{2}$
C $\sqrt{3} / 2$
D $\sqrt{3}$

NDA PREVIOUS YEARS-CIRCLE-MCQs

Home
Ask Doubt
Profile