An equilateral triangle is inscribed in the parabola $y^{2} = 4 a x$ where are at the vertex of the parabola. find the length of the side of the triangle.

Video Solution

Text Solution

Verified by Experts

Equation of parabola $y^{2} = 4 a x$
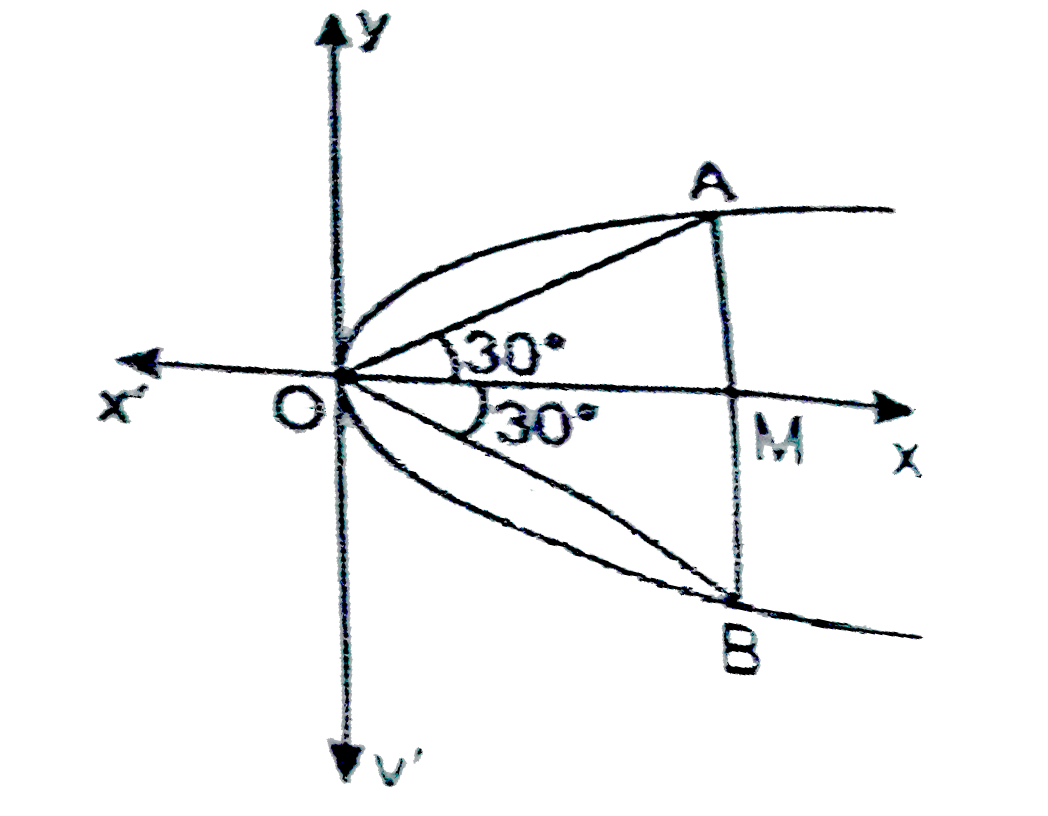
$∴ Vertex O \equiv (0, 0)$
Let OAB is an equilateral triangle whose vertices lie on the given parabola.
In $Δ A M O, ∠ A O B = 60^{\circ}$
$\Rightarrow ∠ A O M = 30^{\circ}$
${sin 30}^{\circ} = \frac{A M}{O A} \Rightarrow \frac{1}{2} = \frac{A M}{O A}$
$\Rightarrow A M = \frac{1}{2} \cdot O A$
$and {cos 30}^{\circ} = \frac{O M}{O A} \Rightarrow \frac{\sqrt{3}}{2} = \frac{O M}{O A}$
$\Rightarrow O M = \frac{\sqrt{3}}{2} O A$
Coordinates of point
$A \equiv (O M, A M)$
$\equiv (\frac{\sqrt{3}}{2} O A, \frac{1}{2} O A)$
This point lies on the parabola $y^{2} = 4 a x$
$\Rightarrow O A = 8 a \sqrt{3}$
$∴ {(\frac{1}{2} O A)}^{2} = 4 a (\frac{\sqrt{3}}{2} O A)$
$\Rightarrow O A = 8 a \sqrt{3}$
$∴$ Length of sides of equilateral triangle $= 8 a \sqrt{3}$ units

Updated on:21/07/2023