An hexagonal pyramid is 20 m high. Side of the baste is 5 m. Find the volume and the slant height of the pyramid.
Given h = 20 m,
Side of base = a = 5 m
∴ Area of base=(√3)(4)×a2×6=6√34×52=3√32×25m2.
Volume =13 Ah, where A = Area of the base and h = Height
=13×3√32(25)×20=√3×250=250√3m3.
To find slant height, refer to the figure shown In the figure,
O is the vertex of the pyramid and G is the centre of the hexagonal base. H is the mid-point of AB.

OG is the axis of the pyramid.
OH is the slant height of the pyramid.
△OGH is a right angled triangle.
∴OH2=GH2+OG2
GH= Altitude of △AGB=√32a=√32×5=5√32m
∴OH2=(5√32)2+(20)2=25×34+400
=75+16004=16754
⇒OH=√16752m
∴ Slant height=√16752m.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Very Short Answer Type Questions30videos
MENSURATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Short Answer Type Questions19videos
MENSURATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MATRICESEXERCISE - EXERCISE CONCEPT APPLICATION (LEVEL 3)15videos
MATRICES
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODULAR ARITHMETIC EXERCISE - Level 315videos
MODULAR ARITHMETIC
Similar Questions
A conical tent is 10m high and the radius of its base is 24m. Find the slant height of the tent. If the cost of 1m2 convas is Rs. 70, find the cost of the canvas required to make the tent.
View SolutionA conical tent is 10m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1m2 canvas is Rs 70, find the cost of canvas required to make the tent.
View Solution
Knowledge Check
- Question 1 - Select One
A prism and a pyramid have the same base and the same height. Find the ratio of the volumes of the prism and the pyramid.
A1:1B1:3C3:1DCannot be determined - Question 2 - Select One
The base of a pyramid is a rectangle 40 m long and 20 m wide. The slant height of the pyramid from the mid-point of the shorter side of the base to the apex is 29 m. What is the volume of pyramid ?
Aa. 5600m3Bb. 400m3Cc. 6500m3Dd. 1753√110m3
A right pyramid is on a regular hexagonal base. Each side of the base is 10 m and the height is 60 m. The volume of the pyramid is (a) 5000 m3 (b) 5100 m3 (c) 5195 m3 (d) 5196 m3
View SolutionA conical tent is 10 m high and the radius of its base is 24 m. Find(i) slant height of the tent.(ii) cost of the canvas required to make the tent, if the cost of 1 m2canvas is Rs 70.
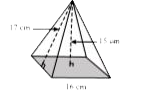
View SolutionFind the total surface area of a pyramid with a square base if each side of the base measures 16 cm, the slant height of a side is 17 cm and the altitude is 15 cm.
 View Solution
View SolutionA rectangular pyramid has a base area of 56cm2 and a volume of 224cm2. What is the height of the pyramid ?
View SolutionThe diagram shows a pyramid on a square base ABCD.The diagonals of the base, AC and BD, intersect at M.The sides of the square are 8 cm and the vertical height of the pyramid, PM, is 5cm.Calculate(a) the length of the edge PB,
View SolutionA conical tent is 10 m high and the radius of its base is 24 m. Find(i) slant height of the tent.(ii) cost of the canvas required to make the tent, if the cost of 1 m2canvas is Rs 70.
View Solution
