Question

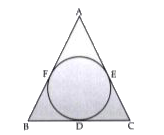
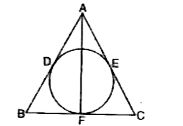
An isosceles triangle ABC, with AB = AC, circumscribes a circle, touching BC at P, AC at Q and AB at R. Prove that the contact point P bisects BC.

Explanation

To prove that the contact point P bisects BC in the isosceles triangle ABC, where AB = AC and the triangle circumscribes a circle, we can follow these steps:

Step 1: Understand the Triangle and Circle
We have an isosceles triangle ABC with AB = AC. The circle touches the sides of the triangle at points P (on BC), Q (on AC), and R (on AB).

Step 2: Assign Tangent Lengths
Since the circle is tangent to the sides of the triangle, we can denote the lengths of the tangents from points B and C to the points of tangency:
- Let AR = x (tangent from A to R)
- Let BR = y (tangent from B to R)
- Let AQ = x (tangent from A to Q)
- Let QC = z (tangent from C to Q)
- Let BP = y (tangent from B to P)
- Let PC = z (tangent from C to P)

Step 3: Use the Tangent Length Property
Using the property of tangents from a point to a circle, we know:
- From point A: AR = AQ = x
- From point B: BR = BP = y
- From point C: QC = PC = z

Step 4: Write Equations Based on Tangents
From the above, we can write:
1. \( AB = AR + BR = x + y \)
2. \( AC = AQ + QC = x + z \)

Since AB = AC, we can set the equations equal to each other:
\( x + y = x + z \)

Step 5: Simplify the Equation
By simplifying the equation, we can cancel x from both sides:
\( y = z \)

Step 6: Conclude that P Bisects BC
Since y = z, we can conclude that:
- BP = y
- PC = z

Thus, we have BP = PC, which means point P bisects segment BC.

Final Conclusion
Therefore, we have proved that the contact point P bisects BC.