In circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
Step by step video & image solution for In Delta ABC, AB = AC. A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTIONS (MCQ.s)14videos
CIRCLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SUM TO ENRICH REMAMBER6videos
CIRCLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - EXERCISE 10.610videos
CIRCLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS3videos
INTRODUCTION TO EUCLID.S GEOMETRY
Similar Questions
In a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View SolutionTwo circles are drawn with sides AB and AC of a triangle ABC as diameters
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D To Prove: BD=DC Construction : Join AD
View SolutionAn isosceles triangle ABC, with AB = AC, circumscribes a circle, touching BC at P, AC at Q and AB at R. Prove that the contact point P bisects BC.
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionIn the given figure, side BC of ΔABC is bisected at D and O is any point AD.BO and CO produced meet AC and AB at E and F respectively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that AO:AX=AF:AB and show that EF∣∣BC.
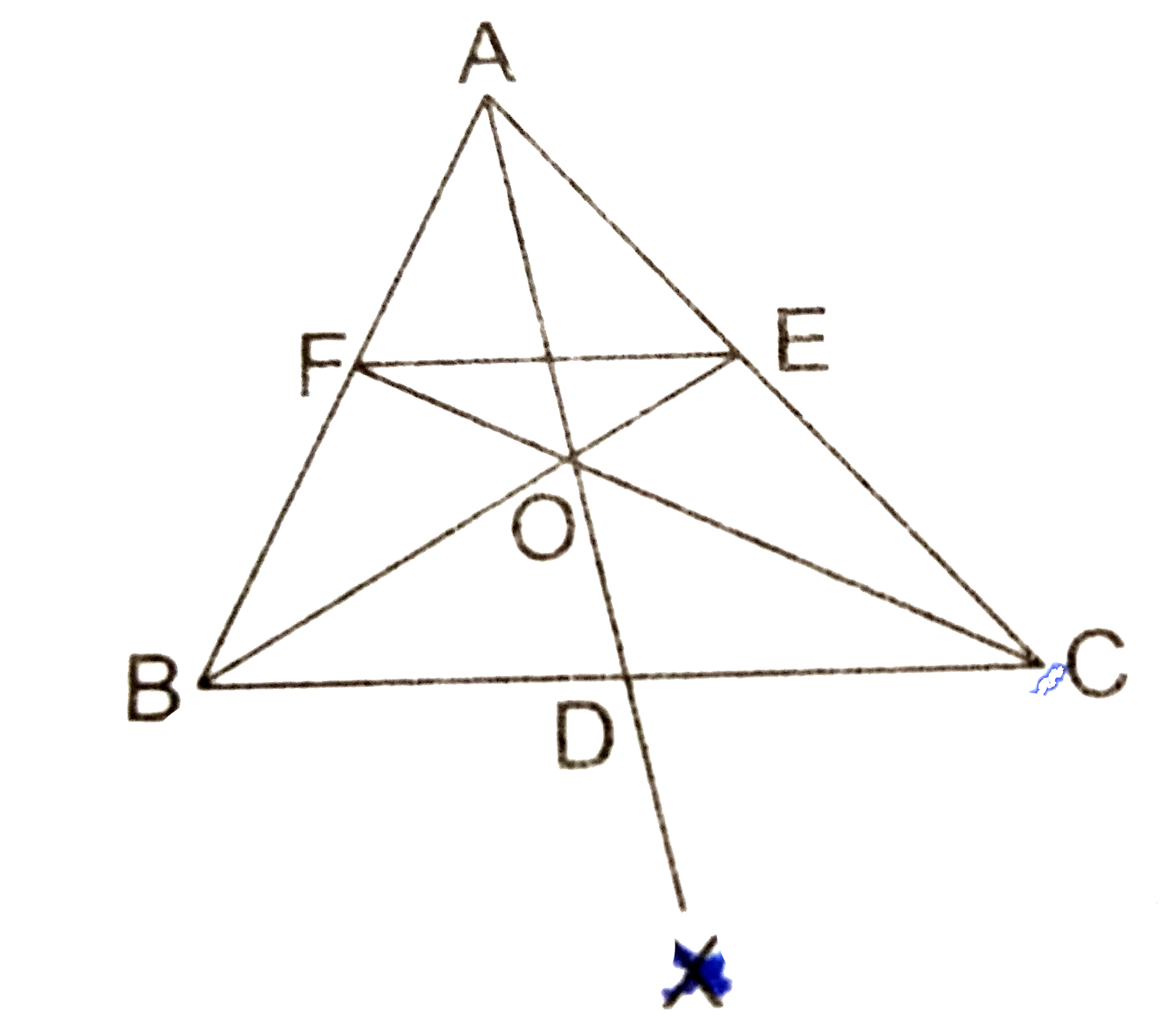 View Solution
View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View Solution

