An ordinary cubical dice having six faces marked with alphabets A, B, C, D, E, and F is thrown n times and ht list of n alphabets showing p are noted. Find the total number of ways in which among the alphabets A, B, C D, E and F only three of them appear in the list.
Three letters from six letters can be selected in 6C3 ways.
Consider one such set of letters {A,B,C}.
Now, if each throw of dice shows either letter A, B or C then number of cases is 3n.
But this includes those cases also in which exactly one letter or exactly two letters from A, B and C appear.
Number of cases in which exactly one letter appears in all throws is 3.
Number of cases in which exactly two letters appear (each at least once) is 3C2(2n−2).
So, required number of cases =6C3×[3n−3C2(2n−2)−3]
Similar Questions
An ordinary cubical dice having six faces marked with alphabets A, B, C, D, E, and F is thrown n times and the list of n alphabets showing up are noted. Find the total number of ways in which among the alphabets A, B, C D, E and F only three of them appear in the list.
View SolutionAn ordinary cubical dice having six faces marked with alphabets A, B, C, D, E, and F is thrown n times and the list of n alphabets showing up are noted. Find the total number of ways in which among the alphabets A, B, C D, E and F only three of them appear in the list.
View Solution
Knowledge Check
Choose the right option in which all the alphabets A, B, C, D and E are correctly identified
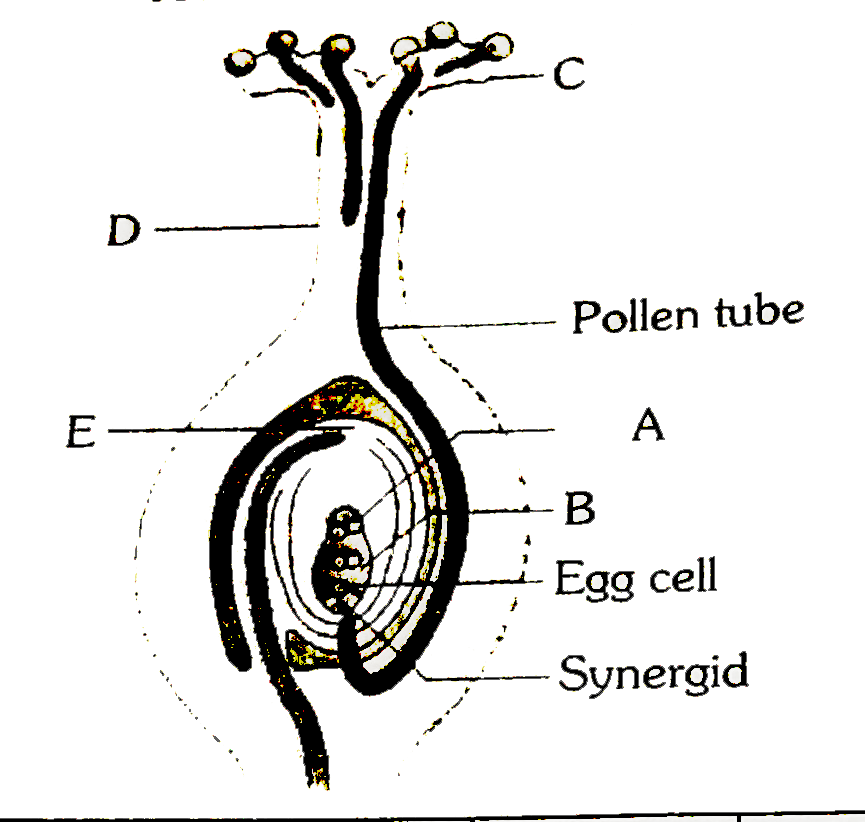 A A B C D E Antipodal cells Secondary nuclei Chalaza Stigma StyleB A B C D E Antipodal cells Secondary nuclei Stigma Chalaza StyleC A B C D E Antipodal cells Secondary nuclei Style Stigma ChalazaD A B C D E Antipodal cells Secondary nuclei Stigma Style Chalaza
A A B C D E Antipodal cells Secondary nuclei Chalaza Stigma StyleB A B C D E Antipodal cells Secondary nuclei Stigma Chalaza StyleC A B C D E Antipodal cells Secondary nuclei Style Stigma ChalazaD A B C D E Antipodal cells Secondary nuclei Stigma Style ChalazaThe six faces of a dice have been marked with the letters A, B, C, D, E and F. If A is adjacent to B, C and E, then which of the following statements is true?
AA is adjacent to D .BA is adjacent to FCB is adjacent to F .DD is adjacent to F .
An unbiased dice, with faces numbered 1,2,3,4,5,6, is thrown n times and the list of n numbers shown up is noted. Then find the probability that among the numbers 1,2,3,4,5,6 only three numbers appear in this list.
View SolutionAn unbiased dice, with faces numbered 1,2,3,4,5,6, is thrown n times and the list of n numbers shown up is noted. Then find the probability that among the numbers 1,2,3,4,5,6 only three numbers appear in this list.
View SolutionAn unbiased dice, with faces numbered 1, 2, 3, 4, 5, 6, is thrown n times and the list of n numbers shown up is noted. Then find the probability that among the numbers 1, 2, 3, 4, 5, 6 only three numbers appear in this list and each number appears at least once.
View SolutionAn unbiased dice, with faces numbered 1, 2, 3, 4, 5, 6, is thrown n times and the list of n numbers shown up is noted. Then find the probability that among the numbers 1, 2, 3, 4, 5, 6 only three numbers appear in this list and each number appears at least once.
View SolutionAn unbiased dike, with faces numbered 1,2,3,4,5,6, is thrown n times and the list of n numbers shown up is noted. Then find the probability that among the numbers 1,2,3,4,5,6 only three numbers appear in this list.
View SolutionA,A,B,B,C,C,D,E,F are arranged in a row so that no two alike alphabets are together. Find number of such arrangment
View Solution
