∠Aand∠B are two complementary angles. If ∠A is 20∘ more than ∠B, then find the angles of ∠Aand∠B.
To solve the problem, we need to find the measures of angle A and angle B, given that they are complementary angles and that angle A is 20 degrees more than angle B.
1. Understand the definition of complementary angles:
Complementary angles are two angles whose sum is 90 degrees.
2. Set up the equations:
- Let angle B be represented as x.
- Since angle A is 20 degrees more than angle B, we can express angle A as x+20.
3. Write the equation for complementary angles:
According to the definition, we have:
Angle A+Angle B=90∘
Substituting the expressions for angle A and angle B, we get:
(x+20)+x=90
4. Combine like terms:
Simplifying the equation:
2x+20=90
5. Isolate the variable:
Subtract 20 from both sides:
2x=90−20
2x=70
6. Solve for x:
Divide both sides by 2:
x=702=35
7. Find angle B:
Since x represents angle B:
Angle B=35∘
8. Find angle A:
Now, substitute x back into the expression for angle A:
Angle A=x+20=35+20=55∘
Final Answer:
- Angle A = 55∘
- Angle B = 35∘
---
Complementary angles are two angles whose sum is 90 degrees.
- Let angle B be represented as x.
- Since angle A is 20 degrees more than angle B, we can express angle A as x+20.
According to the definition, we have:
Angle A+Angle B=90∘
Substituting the expressions for angle A and angle B, we get:
(x+20)+x=90
Simplifying the equation:
2x+20=90
Subtract 20 from both sides:
2x=90−20
2x=70
Divide both sides by 2:
x=702=35
Since x represents angle B:
Angle B=35∘
Now, substitute x back into the expression for angle A:
Angle A=x+20=35+20=55∘
- Angle A = 55∘
- Angle B = 35∘
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
48 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
19 Videos
- FRACTIONS AND DECIMALS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FRACTIONS AND DECIMALS EXERCISE - Crossword
1 Videos
- MENUSRATION BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENUSRATION EXERCISE - Crossword
1 Videos
Similar Questions
Knowledge Check
In a △ABC,∠A=35∘ and ∠B=65∘,find the measure of ∠C
A80∘B120∘C155∘D140∘In figure, ∠B<∠Aand∠C<∠D then
 AAD<BCBOD>OCCOB<OADNone of these
AAD<BCBOD>OCCOB<OADNone of theseIn the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
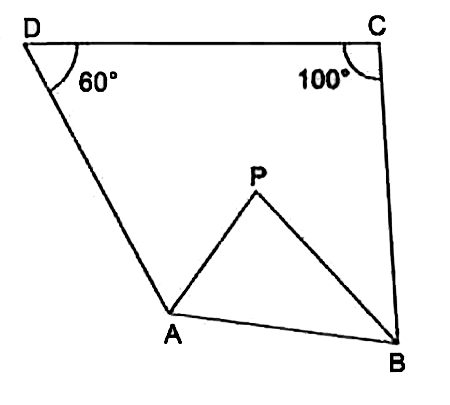 A80∘B100∘C70∘D60∘
A80∘B100∘C70∘D60∘
If ∠A and ∠B are supplementary angles, where ∠A=x+10∘ and ∠B=x−10∘, then find ∠A and ∠B.
View SolutionIf ∠A and ∠B are supplementary angles. If 4∠A=5∠B, then find ∠A and ∠B.
View SolutionIn a triangle ABC, if ∠A=70∘andAB=AC, then find the measures of ∠Band∠C.
View SolutionGiven that ∠A and ∠B are supplementary angles. If ∠A:∠B=7:8, then find ∠A and ∠B.
View SolutionIn a △ABC if ∠A=72∘ and ∠B=63∘,find ∠C
View Solution
