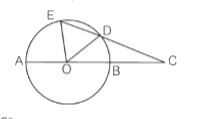
AOD is a diameter of the circle with centre O. Given that ∠BDA=18∘and∠BDC=38∘.∠BCD equals
90∘
108∘
76∘
52∘
The correct Answer is:B
Step by step video, text & image solution for AOD is a diameter of the circle with centre O. Given that angle BDA = 18^(@) and angle BDC = 38^(@).angle BCD equals by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - UNIT TEST - 425videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - QUESTION BANK - 431videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET10videos
AVERAGE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Self Assessment Sheet10videos
CO-ORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, BOD is the diameter of the circle with centre O. ∠COD=92∘and∠ABD=65∘. Then y equals
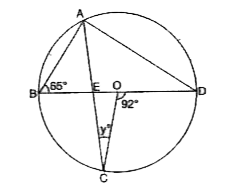 A65∘B46∘C44∘D21∘
A65∘B46∘C44∘D21∘ - Question 2 - Select One
O is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
 A150∘B210∘C75∘D105∘
A150∘B210∘C75∘D105∘ - Question 3 - Select One
ED is the tangent to the circle with centre O. ∠BCD=52∘. Then, ∠ CAB equals
 A38∘B76∘C52∘D46∘
A38∘B76∘C52∘D46∘
In the figure XY is a tangent to the circle with centre O at A. If ∠BAX=70∘,∠BAQ=40∘ then ∠ABQ is equal to :
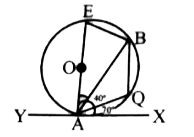 View Solution
View SolutionPBA and PDC are two secants. AD is the diameter of the circle with centre at O. ∠A=40∘,∠P=20∘. Find the measure of ∠DBC.
 View Solution
View SolutionPQ is the diameter of the given circle, whose centre is O. Given, ∠Ros=54∘, calculate ∠RTS.
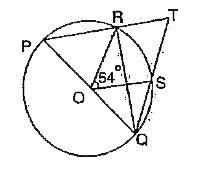 View Solution
View SolutionIn the diagram, CB and CD are tangents to the circle with centre O. AOC is a straight line and ∠OCB=34∘.∠ABO equals.
 View Solution
View SolutionIn the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
View Solution