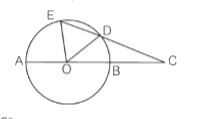
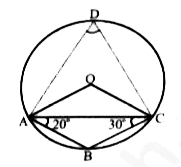
PBA and PDC are two secants. AD is the diameter of the circle with centre at O. ∠A=40∘,∠P=20∘. Find the measure of ∠DBC.

45∘
30∘
60∘
75∘
The correct Answer is:B
Step by step video & image solution for PBA and PDC are two secants. AD is the diameter of the circle with centre at O. angle A = 40^(@), angle P = 20^(@). Find the measure of angle DBC. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
AOD is a diameter of the circle with centre O. Given that ∠BDA=18∘and∠BDC=38∘.∠BCD equals
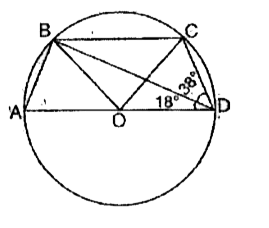 A90∘B108∘C76∘D52∘
A90∘B108∘C76∘D52∘In the given figure, BOD is the diameter of the circle with centre O. ∠COD=92∘and∠ABD=65∘. Then y equals
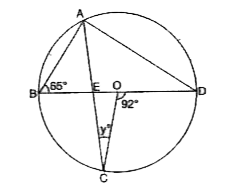 A65∘B46∘C44∘D21∘
A65∘B46∘C44∘D21∘If O is the centre of the circle then find ∠ADC
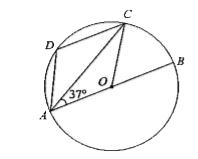 A125∘B127∘C90∘D137∘
A125∘B127∘C90∘D137∘
In the following figures, AB be diameter of a circle whose centre is O. If ∠AOE=150∘,∠DAO=51∘, then the measure of ∠CBE is-
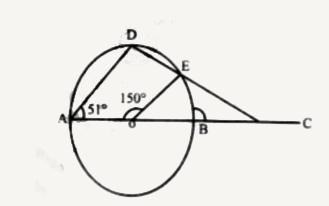
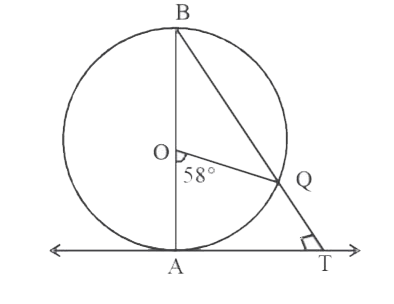
View SolutionAB is a diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘ find ∠ATQ.
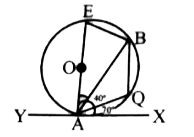
View SolutionIn the figure XY is a tangent to the circle with centre O at A. If ∠BAX=70∘,∠BAQ=40∘ then ∠ABQ is equal to :
View SolutionTP and TQ are the tangents from the external point T of a circle with centre O. If ∠OPQ=30∘ then find the measure of ∠TQP.
View SolutionIn the figure, O is centre of a circle. If ∠BAC=20∘and∠ACB=30∘. Find ∠AOC
View Solution