Area and Perimeter of rhombus
Area and Perimeter of Rhombus
Rhombus is a 2-Dimensional quadrilateral shape with four equivalent sides and four interior angles that are not necessarily 90 degrees. The sum of lengths of all the four sides of a rhombus is the perimeter of a rhombus. A square is also a type of rhombus because it fulfils all the condition that a rhombus possesses.
In a rhombus:
• All four sides are of the same length
• Opposite sides are parallel.
• The height is a distance at right angles to two opposite sides.
• Diagonals bisect each other at 90 degrees.
Area of a Rhombus
The area of a rhombus can be characterized as the measure of space enclosed by a rhombus on a flat surface or in a two-dimensional space. A rhombus is a quadrilateral with four equal sides where two pair of opposite sides are parallel. It is also known as symmetrical quadrilateral because all its four sides are equivalent.
How to find the Area of Rhombus?
There are different methods to calculate the area of a rhombus. There are three different formulae for rhombus area:
- Using Base and Height
- Using Diagonals
- Using Trigonometry
Area of Rhombus Formula
There are various formulas to find the area of a rhombus :
Different Formulas to Find Area of Rhombus
Base and Height
A = s × h
Diagonals
A = ½ × d1 × d2
Trigonometry
A = b2 × Sin(x)
Where,
- s à length of any side
- h à height of rhombus
- d1 à length of diagonal 1
- d2 à length of diagonal 2
- x à any interior angle of the rhombus
Area of Rhombus with Base (any side of rhombus) and height
First, we will find the base (side of a rhombus) and the perpendicular height of the rhombus. Then we will multiply the base and height.
Example 1: Find the area of a rhombus if its base is 9 cm and height is 6 cm.
Solution:
Given,
Base, b = 9 cm
Height, h = 6 cm
Area, A = b × h
= 9 × 6 cm2
Area of rhombus= 54 cm2
Area of Rhombus with Diagonals
Suppose a rhombus PQRS, having two diagonals, i.e. d1= PR & d2=QS.
First we will find the length of d1. It is the distance between P and R. The diagonals of a rhombus intersect each other at right angles making 4 right triangles at the centre of the rhombus. Second, we will find the length of d2, which is the distance between Q and S. Then multiply both the diagonals, d1 and d2. Finally, divide the result by 2.
Example 2: Find the area of a rhombus whose diagonals are 10 cm and 12 cm long.
Solution:
Given ,
Diagonal 1, d1 = 10 cm
Diagonal 2, d2 = 12 cm
Area of a rhombus = (d1 × d2) / 2
= (10 × 12) / 2
= 120 / 2
= 60 cm2
Thus, Area of a rhombus is 60 cm2.
Area of Rhombus Using Trigonometry
In this case, first, we have to square the length of any of the sides, and then multiply it by Sine of any interior angles.
Example 3 Determine the area of a rhombus if the length of its side is 4 cm and one of its angle A is 30 degrees.
Solution:
Given,
Side, a = 4 cm
Angle A = 30 degrees
square of side a = 4 × 4= 16 cm2
Area, A= s2 × sin (30)
A= 16 × 1/2
Area of rhombus = 8 cm2
Formula for Perimeter of a Rhombus
Perimeter of any geometrical shape is the total distance covered around the boundary, which can be determined by the algebraic sum of the length of each side. In a rhombus, all four sides have equivalent length; therefore, the perimeter becomes four times the length of a side.
Perimeter of Rhombus = 4 x Side
Related Videos:
- Area and Perimeter of rectangle
- Area and Perimeter of square
- Area and Perimeter of Trapezium
- Area and Perimeter of parallelogram
- Area and Perimeter of triangle
- Area and Perimeter of circle
Solved Problems on Rhombus Area and Perimeter Formula
Question 1: Find the perimeter of a rhombus having side as 6 cm ?
Solution:
Given,
a = 6 cm
Perimeter of a rhombus = 4 × a
Perimeter of a rhombus = 4 × 6
Perimeter of a rhombus = 24 cm
Question 2: Find the area of the rhombus having each side equal to 10 cm and one of its diagonals equal to 12 cm.
Solution:
ABCD is a rhombus in which AB = BC = CD = DA = 10 cm
Diagonal AC = 12 cm (with O being the intersection median point of the diagonal)
Therefore, AO = 6 cm
In ∆ AOD,
AD2 = AO2 + OD2
⇒ 102 = 62 + OD2
⇒ 100 -36 = OD2
⇒ 64 = OD2
⇒ OD = 8
Therefore, BD = 2 × OD
= 2 × 8
= 16 cm
Now, area of rhombus
= ½ × d1 × d2
= ½ × 12 × 16
Area of rhombus = 96 cm2
Question 3: The lengths of the diagonals of a rhombus are 20 and 48 meters. Find the perimeter of the rhombus.
Solution: Applying the Pythagorean theorem to triangle BOC
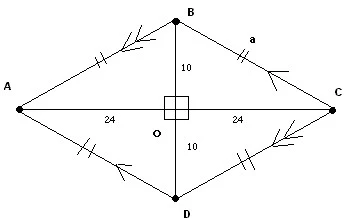
BC 2 = 10 2 + 24 2
BC2 = 100 + 576 m
BC2 = 676 = 26 m
Perimeter of Rhombus = 4 x side
= 4 x 26 m = 104 m
Question 4: Find the length of the diagonal of a rhombus if its area is 100 cm2 and length of one diagonal is 20 cm.
Solution:
Given: Area of rhombus = 100 cm2 and Lets say d1 = 20 cm.
Area of the rhombus, A = (d1 x d2)/2,
100 = (20 x d2)/2
100 = 10 x d2
or 10 = d2
Important Chapters:
Different Formulas to Find Area of Rhombus
Base and Height
A = s × h
Diagonals
A = ½ × d1 × d2
Trigonometry
A = b2 × Sin(x)
a = 6 cm
Perimeter of a rhombus = 4 × 6
Perimeter of a rhombus = 24 cm
Solution: Applying the Pythagorean theorem to triangle BOC

BC 2 = 10 2 + 24 2
Similar Questions
Knowledge Check
If the diagonal of a rhombus are 24 cm and 10 cm, then the area and perimeter of the rhombus are respectively
A120 sq cm, 52 cmB240 sq cm, 52 cmC120 sq cm, 64 cmD240 sq cm, 64 cmIf the perimeter of a rhombus is 4p and length of its diagonals are a and b , then its area is :
AabBab2CabpDp(a2+b2)If the perimeter of a rhombus is 4a and the lengths of the diagonals are x and y, then its area is
Aa(x+y)Bx2+y2CxyD12xy
Area and Perimeter of all type of parallelogram and rhombus
View SolutionFind the perimeter of a rhombus ,the lengths of whose diagonal are 16cm and 30 cm.
View SolutionThe diagonals of a rhombus are 48 cm and 20 cm long. Find (i) the area of the rhombus and (ii) the perimeter of the rhombus.
View SolutionIf the perimeter of a rhombus is 4a and the length of the diagonals are xandy, then its area is
View SolutionIf the perimeter of a rhombus is 4p and length of its diagonals are a and b , then its area is :
View Solution
