Arnav scored 63 marks in English, 57 in Hindi, 82 in Mathematics, 55 in Social Science and x in Science. If the average he scored is 60, find the average of best four of them.
The correct Answer is:64.25
To solve the problem step by step, we will first find the value of x (the marks scored in Science) and then calculate the average of the best four subjects.
Step 1: Set up the equation for the average
The average score is given by the formula:
Average=Sum of all marksNumber of subjects
In this case, the average is 60, and there are 5 subjects. Therefore, we can write:
60=63+57+82+55+x5
Step 2: Calculate the sum of known marks
Now, let's calculate the sum of the known marks:
63+57+82+55=257
So, we can rewrite the equation as:
60=257+x5
Step 3: Multiply both sides by 5
To eliminate the fraction, multiply both sides by 5:
300=257+x
Step 4: Solve for x
Now, isolate x:
x=300−257
x=43
Step 5: List all the scores
Now we have all the scores:
- English: 63
- Hindi: 57
- Mathematics: 82
- Social Science: 55
- Science: 43
Step 6: Identify the best four scores
The scores in descending order are:
- Mathematics: 82
- English: 63
- Hindi: 57
- Social Science: 55
- Science: 43
The best four scores are:
- 82, 63, 57, and 55.
Step 7: Calculate the average of the best four scores
Now we can calculate the average of the best four scores:
Average of best four=82+63+57+554
Calculating the sum:
82+63+57+55=257
Now, divide by 4:
Average=2574=64.25
Final Answer
The average of the best four subjects is:
64.25
The average score is given by the formula:
Average=Sum of all marksNumber of subjects
In this case, the average is 60, and there are 5 subjects. Therefore, we can write:
60=63+57+82+55+x5
Now, let's calculate the sum of the known marks:
63+57+82+55=257
So, we can rewrite the equation as:
60=257+x5
To eliminate the fraction, multiply both sides by 5:
300=257+x
Now, isolate x:
x=300−257
x=43
Now we have all the scores:
- English: 63
- Hindi: 57
- Mathematics: 82
- Social Science: 55
- Science: 43
The scores in descending order are:
- Mathematics: 82
- English: 63
- Hindi: 57
- Social Science: 55
- Science: 43
- 82, 63, 57, and 55.
Now we can calculate the average of the best four scores:
Average of best four=82+63+57+554
Calculating the sum:
82+63+57+55=257
Now, divide by 4:
Average=2574=64.25
The average of the best four subjects is:
64.25
Topper's Solved these Questions
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Exercise ( Subjective Problems ) ( Long Answer Type )
6 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Exercise ( Integer/Numerical Value Type )
10 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Exercise ( Subjective Problems ) (Very Short Answer Type )
10 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - Olympiad/HOTS CORNER
15 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - OLYMPAID/ HOTS CORNER
10 Videos
Similar Questions
Arun scored 36 marks in English , 44 marks in Hindi, 75 marks in mathemations and x marks in science . If the has secured an average of 50 marks, five the value of x.
View SolutionA student obtained 60 marks in English, 75 in Hindi, 63 in Mathematics, 59 in Economics and 55 in Statistics. Calculate weighted mean of the marks if weights are respectively 2, 1, 5, 5 and 3.
View Solution
Knowledge Check
The given pie- chart shows the marks scored by a students in five different subjects - English, Hindi, Mathematics, Science and Social Science. Assuming that the total marks obtained for the examination are 540 , find the subject in which the student scored 22.2% marks
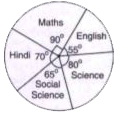 AHindiBScienceCSocial ScienceDEnglish
AHindiBScienceCSocial ScienceDEnglish
A student obtained 60 marks in English, 75 in Hindi, 63 in Mathematics, 59 in Economics and 55 in Statistics. Calculate weighted mean of the marks if weights are respectively 2, 1, 5, 5 and 3.
View SolutionThe adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science.
If the total marks obtained by the students were 540, answer the following questions.
(i)In which subject did the student score 105 marks?
(Hint: for 540 marks, the central angle =360∘. So, for 105 marks, what is the central angle?)
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii)Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi (Hint: Just study the central angles).
View SolutionAmbika got 99 per cent marks in Mathematics, 76 per cent marks in Hindi, 61 per cent in English, 84 per cent in Science, and 95% in Social Science. If each subject carries 100 marks, then find the percentage of marks obtained by Ambika in the aggregate of all the subjects.
View SolutionDirections :- The following pie-chart gives the marks scored by astudent in different subjects— English, Hindi,Mathematics, Science and Social Science in an examination. Assuming that the total marks obtained for the examination are 540, answer the questions.
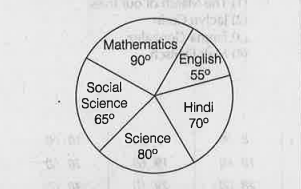
The marks scored in English, Science and Social Science exceed the marks scored in Hindi and Mathematics by
View SolutionAnjali scores 100 marks in Mathematics and x marks in Science. what is her total score in Science and Mathematics?
View SolutionRanjit scores 80 marks in English and x marks in Hindi. What is his total score in the two subjects?
View SolutionRahul scores 80 marks in English and x marks in Hindi. What is his total score in the two subjects?
View Solution
