As shown in the figure, three circles which have the same radius r,have centres at (0,0);(1,1)and(2,1). If they have a common tangentline, as shown then, their radius 'r' is -
The correct Answer is:5

The equation of the line joining the origin and the center of circle C2,(2,1) , is
y=x2
or x−2y=0
Let the equation of common tangent be
x−2y+c=0 (1)
∴ Perpendicular distance from (0,0) on this line
= Perpendicular distance from (1,1)
or ∣∣∣c√5∣∣∣=∣∣∣c−1√5∣∣∣
or c=1−c or c=12
The equation of common tangent is
x−2y+12=0 or 2x−4y+1=0 (2)
The length of perpendicular from (2,1) on the line (2) is
r=∣∣∣4−4+1√20∣∣∣=12√5=√510
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Main Previous Year
10 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
As shown in the figure, three circles which have the same radius r,have centres at (0,0);(1,1)and(2,1). If they have a common tangentline, as shown then, their radius 'r' is -
View SolutionIf two circles of the same radius r and centres at (−1,2) and (3,6) respectively cut orthogonally, then the value of r is
View Solution
Knowledge Check
Find an equation of the circle with centre at (0,0) and radius r.
Ax2+y2=r2Bx2−y2=r2Cx2−r2=y2DNone of theseIn the figure, when the outer circles all have radii 'r', then the radius of the inner circle will be
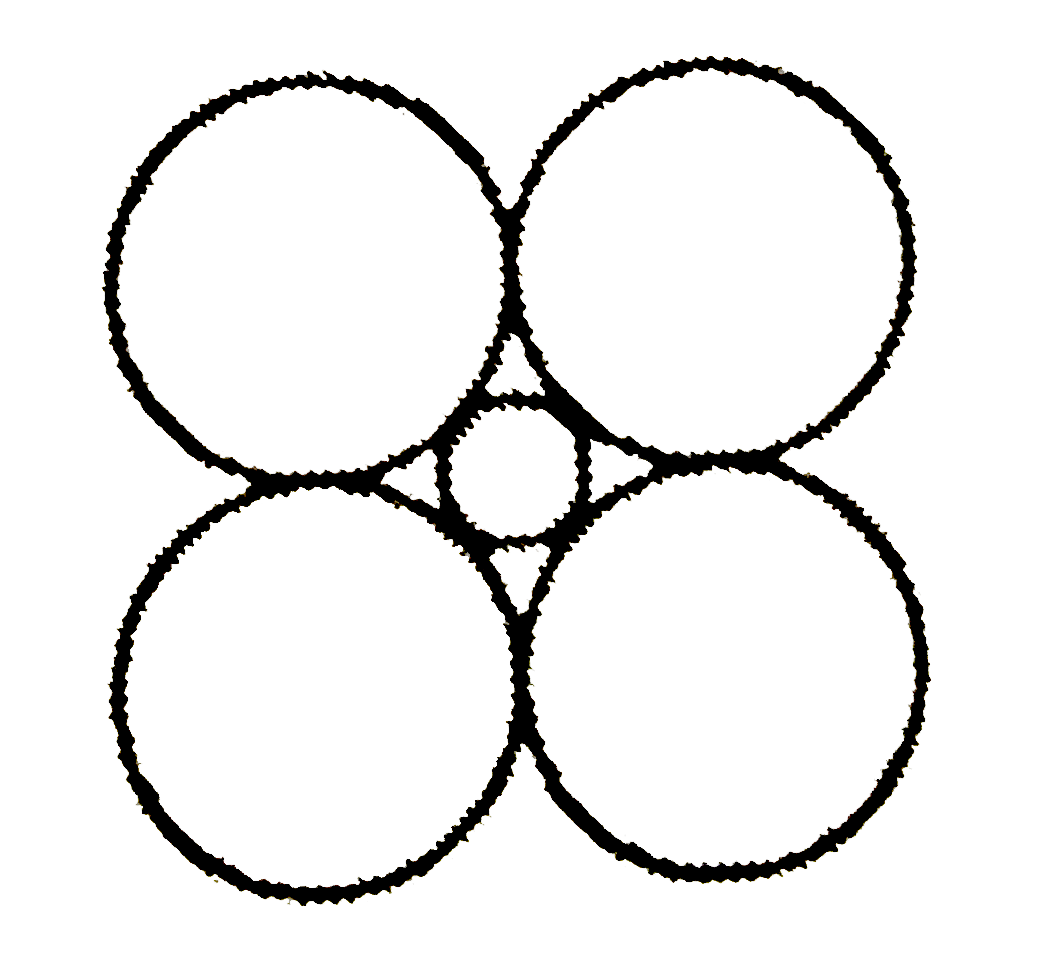 A√2rB(√2−1)rC1√2rD2(√2−1)r
A√2rB(√2−1)rC1√2rD2(√2−1)r
Find an equation of the circle with centre at (0,0) and radius r.
View SolutionAs shown in the figure , the five circles are tangent to one another consecutively and to the lines L1andL2. If the radius of the largest circle is 18 and that of smallest is 8. If radius of middle circle is r, then find the value of r/2
View SolutionA circle centered at P with radius 4 cm and another circle centered at Q with radius 16 cm toucheach other externally. A third circle with centre Ris drawn to touch the first two circles and oneof their common tangents as shown in the figure. Then, the radius of the circle with centre R is:
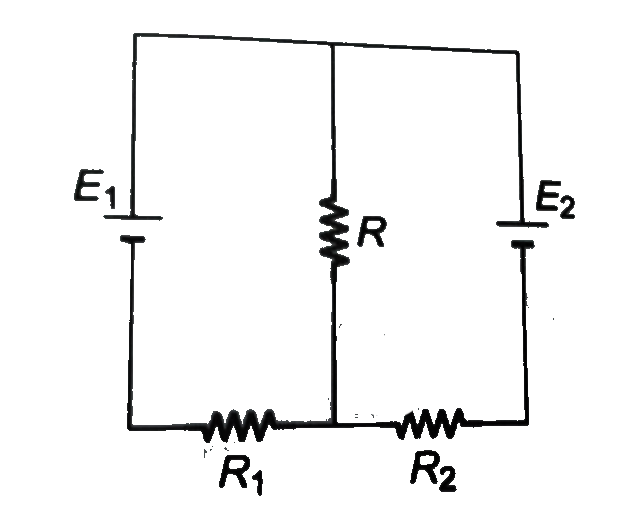
View SolutionIn the circuit shown in figure, the emfs of batteries are E1, and E2 which have internal resistances R1, and R2. At what value of the resistance R will the thermal power generated in it be the highest? What it is?
View SolutionTwo circles of radius r1andr2 touches externally at point A have a common tangent PQ. Then find the value of PQ2.
View SolutionThere are 4 circles on the figure. Two of them have radius 2 and the smallest one has radius 1. If the area of the dashed part is equal to the area of the filled part then find the radius of the largest circle. r
View Solution
