As shown in the figures, two poles of height 8m and 4m are perpendicular to the groudn. If the length of shadow smaller pole due to sunlight is 6 m then long will be the shadow of the bigger pole of the same time?

Video Solution

Text Solution

Verified by Experts

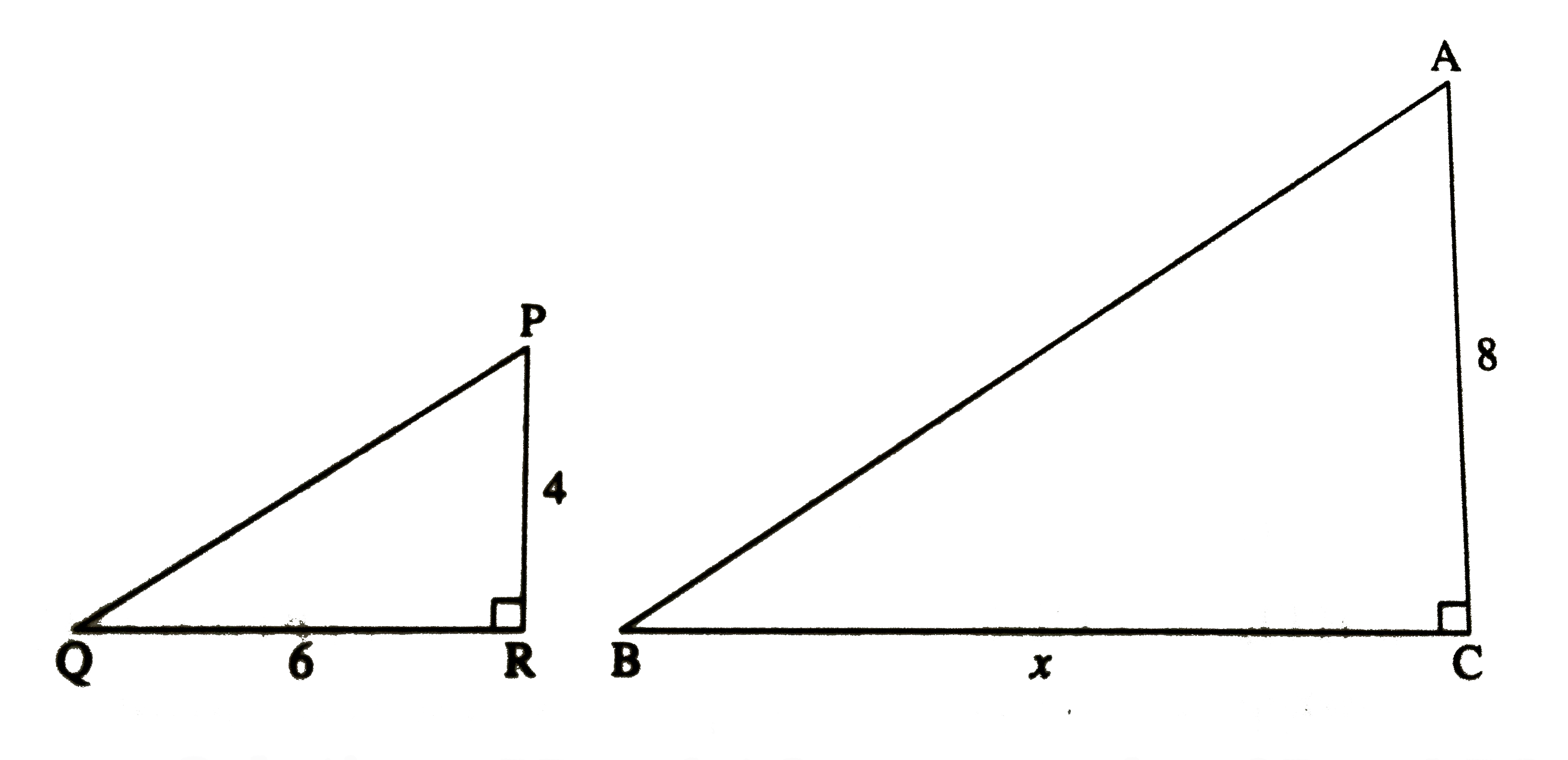
$P r$ and $A C$ are two poles who have their shadows as $Q R$ and $B C$ respectively.
The shadows are formed at the same time.
$∴ Δ P Q R ~ Δ A B C$
$∴ \frac{P R}{A C} = \frac{Q R}{B C}$
$∴ \frac{P R}{A C} = \frac{Q R}{B C}$ ……[Corresponding sides of similar triangles are proportional]
$∴ \frac{4}{8} = \frac{6}{x}$
$∴ 4 \times x = 8 \times 6 ∴ x = \frac{8 \times 6}{4}$
$∴ x = 12 : B C = 12 m$

Updated on:21/07/2023