Assertion (A) : In a trapezium ABCD, we have AB ||DC and the diagonals AC and BD intersect at O.
Then, .
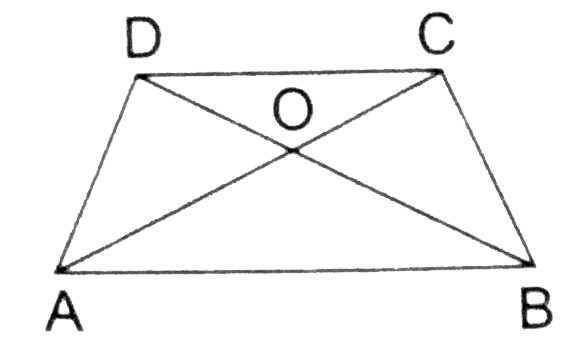
Reason (R ) : Triangle on the same base between the same parallels are equal in area.
Both Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).
Both Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).
Assertion (A) is true and Reason (R ) is false.
Assertion (A) is false and Reason (R ) is true.
The correct Answer is:A
Clearly, Reason (R ) is true.
In trapezium ABCD, we find the are on the same base and between the same parallels.
Assertion (A) is true. And, clearly Reason (R ) gives Assertion (A). Hence, the correct answer is (a).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
In a trapezium ABCD, the diagonals AC and BD interserted other at O such that OB:OD=3:1 then the ratio of area of ΔAOB:ΔCOD is :
A3:1B1:4C9:1Dcan't be determinedIn the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
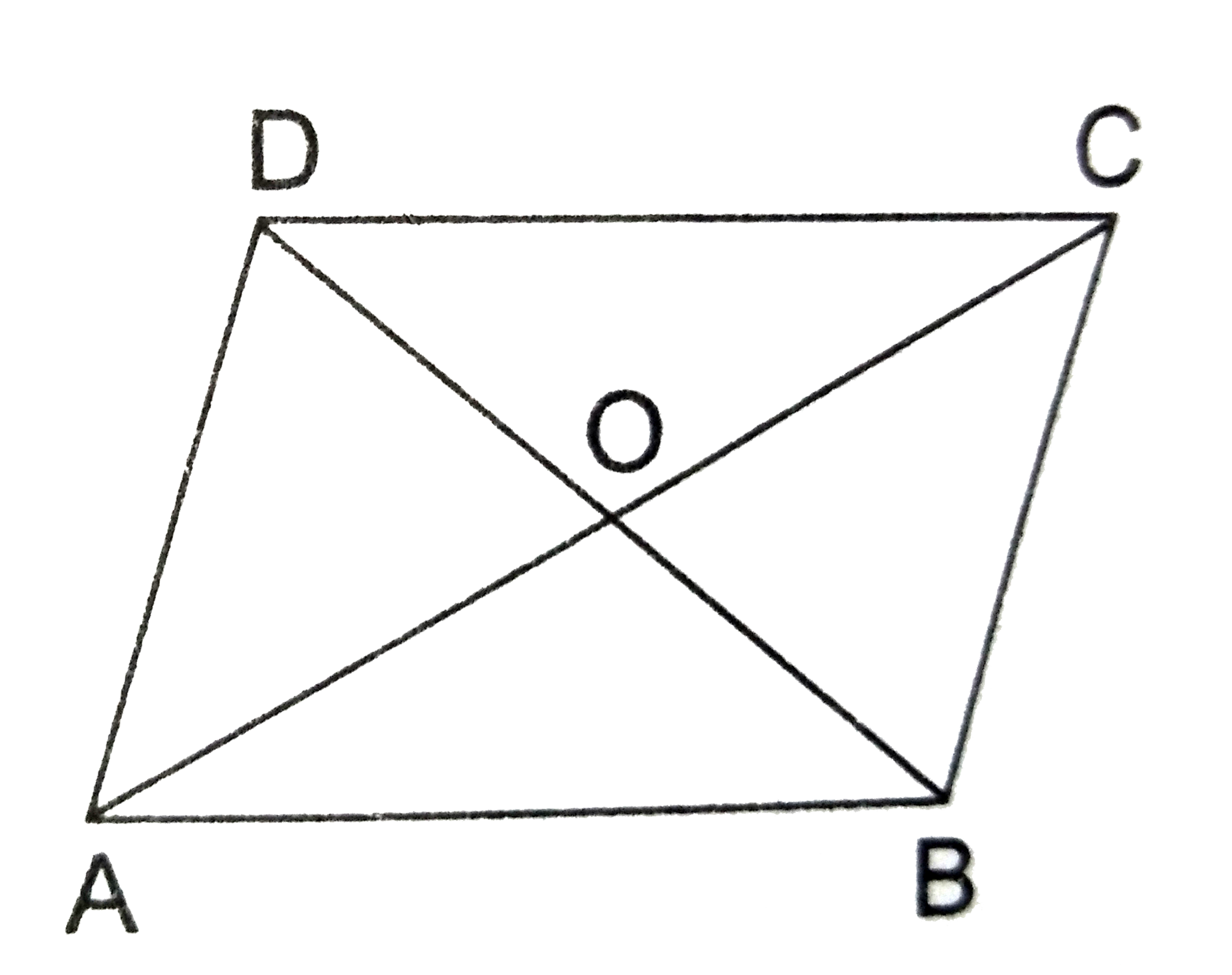 A26cm2B18.5cm2C39cm2D13cm2
A26cm2B18.5cm2C39cm2D13cm2
Parallelograms on the same base and between the same parallel are equal in area.
View SolutionProve that parallelograms on the same base and between the same parallels have the same area.
View SolutionIn trapezium ABCD side AB∣∣ side DC, diagonals AC and BD intersect In point O. If AB=20,DC=6,OB=15 thn find OD.
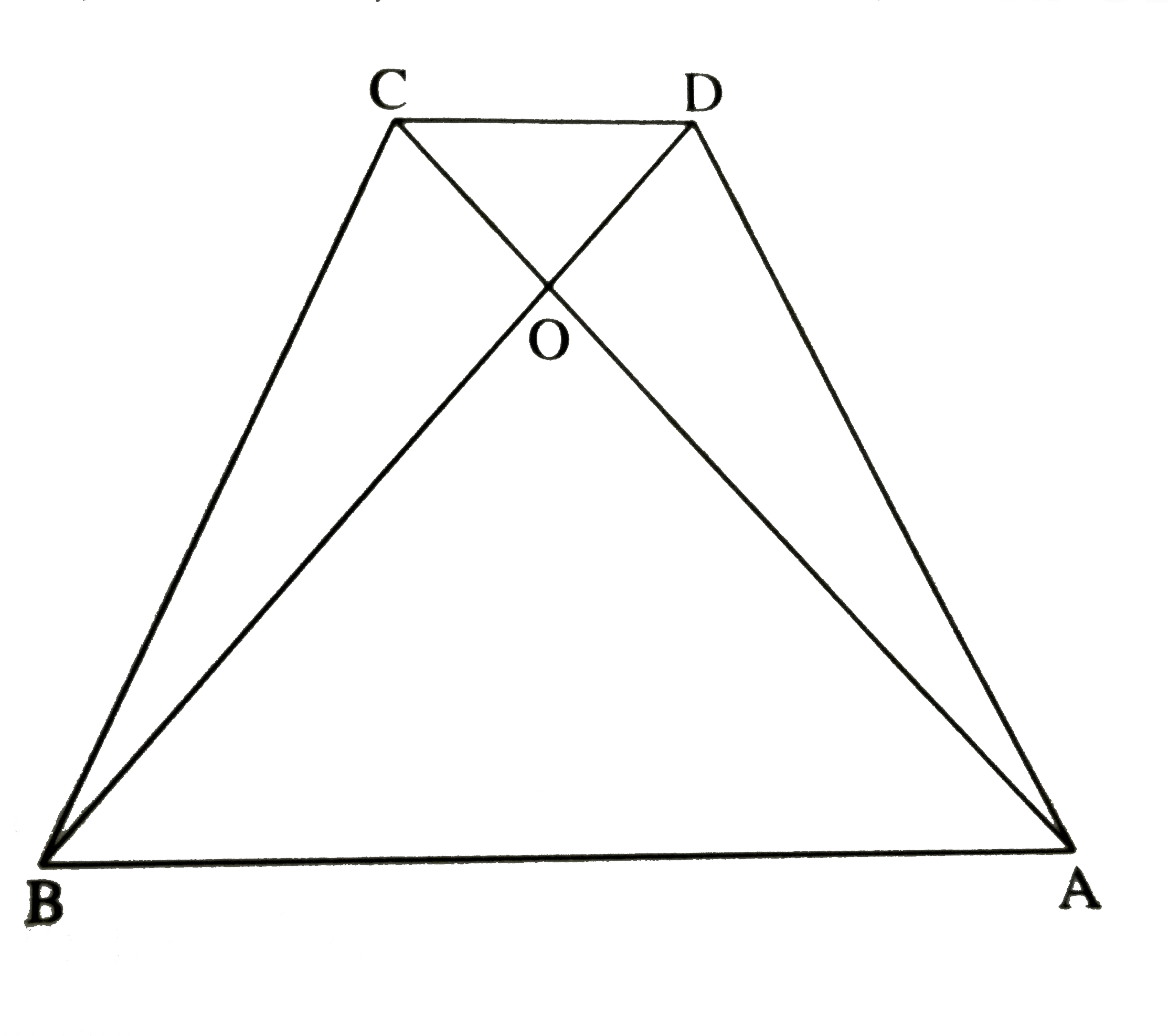
View SolutionThe sides AD, BC of a trapezium. ABCD are parallel and the diagonals AC and BD meet at O. If the area of triangle AOB is 3 cm and the area of triangle BDC is 8 cm2, then what is the area of triangle AOD?
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionIn a trapezium ABCD , it is given that AB∣∣CDandAB=2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB)=84cm2. Find ar(ΔCOD)
View Solution
