The sides AD, BC of a trapezium. ABCD are parallel and the diagonals AC and BD meet at O. If the area of triangle AOB is 3 cm and the area of triangle BDC is 8 cm2, then what is the area of triangle AOD?
8cm2
5cm2
3.6cm2
1.8cm2
To find the area of triangle AOD in trapezium ABCD where AD and BC are parallel, we can use the information given about the areas of triangles AOB and BDC.
1. Identify the Areas Given:
- Area of triangle AOB = 3 cm²
- Area of triangle BDC = 8 cm²
2. Label Areas of Other Triangles:
- Let the area of triangle AOD be denoted as S4.
- Let the area of triangle BOC be denoted as S2.
- Let the area of triangle COD be denoted as S3.
3. Establish Relationships:
- Since triangles AOB and COD share the same height from point O to line AD (the base), and triangles BOC and AOD share the same height from point O to line BC (the base), we can establish that:
S1=S3(Area of AOB and COD)
- Therefore, S1=3 cm² implies S3=3 cm².
4. Use Area of Triangle BDC:
- The area of triangle BDC can be expressed as:
Area of BDC=S2+S3
- Substituting the known values:
8=S2+3
- Thus, we find:
S2=8−3=5 cm²
5. Relate Areas Using Ratios:
- Since triangles AOB and AOD are on the same base AD and between the same parallels, we can use the ratio of their areas:
S1S4=S2S3
- Substituting the known values:
3S4=53
6. Cross-Multiply to Solve for S4:
- Cross-multiplying gives:
3⋅3=5⋅S4
- Therefore:
9=5S4
- Solving for S4:
S4=95=1.8 cm²
Final Answer:
The area of triangle AOD is 1.8 cm².
- Area of triangle AOB = 3 cm²
- Area of triangle BDC = 8 cm²
- Let the area of triangle AOD be denoted as S4.
- Let the area of triangle BOC be denoted as S2.
- Let the area of triangle COD be denoted as S3.
- Since triangles AOB and COD share the same height from point O to line AD (the base), and triangles BOC and AOD share the same height from point O to line BC (the base), we can establish that:
S1=S3(Area of AOB and COD)
- Therefore, S1=3 cm² implies S3=3 cm².
- The area of triangle BDC can be expressed as:
Area of BDC=S2+S3
- Substituting the known values:
8=S2+3
- Thus, we find:
S2=8−3=5 cm²
- Since triangles AOB and AOD are on the same base AD and between the same parallels, we can use the ratio of their areas:
S1S4=S2S3
- Substituting the known values:
3S4=53
- Cross-multiplying gives:
3⋅3=5⋅S4
- Therefore:
9=5S4
- Solving for S4:
S4=95=1.8 cm²
The area of triangle AOD is 1.8 cm².
Similar Questions
Knowledge Check
- Question 1 - Select One
In the following figure, PQ is parallel to BC and PQ:BC=1:3. If the area of the triangle ABC is 144cm2, then what is the area of the triangle APQ?
 A48cm2B36cm2C16cm2D9cm2
A48cm2B36cm2C16cm2D9cm2 - Question 2 - Select One
In trapezium ABCD, AB || CD and AB = 2 CD. Its diagonals intersect at O. If the area of ΔAOB=84cm2, then the area of ΔCOD is equal to
A72cm2B21cm2C42cm2D26cm2 - Question 3 - Select One
In triangle ABC, AD, BE and CF are the medians intersecting at point G and area of triangle ABC is 156cm2. What is the area (in cm2) of triangle FGE ?
A13B26C39D52
In the following figure, PQ is parallel to BC and PQ:BC=1:3. If the area of the triangle ABC is 144cm2, then what is the area of the triangle APQ?
 View Solution
View SolutionThe diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the triangle CPD ?
View SolutionIf area of Parallelogram ABCD is 80cm2 Find the area of ΔAPD.
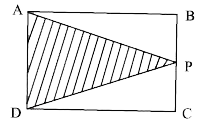 View Solution
View SolutionIn the given figure ratio of AD:DC=3:2 and area of triangle ABC is 40cm^2. Then find the value of area of triangle BDC
View SolutionABCD is a square , E is a point on AB such that BE=17 cm. The area of triangle ADE is 84 cm2 . What is the area of square ?
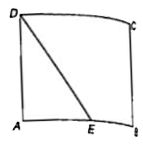 View Solution
View Solution

