At 10.00 A.M. a woman took a cup of hot instant coffe from her microwave oven and placed it on a nearby Kitchen counter to cool. At this instant the temperature of the coffee was 180∘F, and 10 minutes later it was 160∘F. Assume that constant temperature of the kitchen was 70∘F.
(i) What was the temperature of the coffee at 10.15 A.M. ? Solution in Tamil
The correct Answer is:(i) 151.39
(ii) 22.523
Step by step video, text & image solution for At 10.00 A.M. a woman took a cup of hot instant coffe from her microwave oven and placed it on a nearby Kitchen counter to cool. At this instant the temperature of the coffee was 180^(@)F, and 10 minutes later it was 160^(@)F. Assume that constant temperature of the kitchen was 70^(@)F. (i) What was the temperature of the coffee at 10.15 A.M. ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ORDINARY DIFFERENTIAL EQUATIONS BOOK - FULL MARKSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - EXERCISE 10.9
25 Videos
- ORDINARY DIFFERENTIAL EQUATIONS BOOK - FULL MARKSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - ADDITIONAL PROBLEMS
40 Videos
- ORDINARY DIFFERENTIAL EQUATIONS BOOK - FULL MARKSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - EXERCISE 10.7
15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - FULL MARKSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE -4.6
20 Videos
- PROBABILITY DISTRIBUTIONSBOOK - FULL MARKSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - Additional Problems
27 Videos
Similar Questions
The order and degree of the differential equation d2ydx2+(dydx)13+x14=0 are respectively.
View SolutionFind the order and degree of the following differential equations
(i) dydx+y=x2
(ii) y'+y2=x
(iii) y'+3y2+y3=0
(iv) d2ydx2+x=√y+dydx
(v) d2ydx2−y+dydx+d3y(dx3)32=0
(vi)y'=(y−y'3)2/3
(vii)y'+(y2)=(x+y2)
(viiii)y'+(y)2=x(x+y)2 (ix)dy(dx)2+x=dxdy+x2
(x) sinx(dx+dy)=cosx(dx−dy)
View SolutionSolve the following Linear differential equations :
cosxdydx+ysinx=1
View SolutionThe value of sin−1(cosx),0≤x≤π is :
View SolutionFour defective oranges are accidentally mixed with sixteen good ones . Two oranges are drawn at random from the mixed lot. If the random variable X denotes the number of defective oranges then find the values of X and number of points in its iverse image.
View SolutionNewton's law of cooling states that the rate of change of the temperature T of an object is proportional to the difference between T and the (constant) temperature τ of the surrounding medium, we can write it as dTdt=−k(T−τ)k>0 constant
An cup of coffee is served at 185∘F in a room where the temperature is 65∘F. 2 minutes later the temperature of the coffee has dropped to 155∘F.
loge3=1.09872,loge.34=0.2877
The temperature of any object at t = 2 is
View SolutionNewton's law of cooling states that the rate of change of the temperature T of an object is proportional to the difference between T and the (constant) temperature τ of the surrounding medium, we can write it as dTdt=−k(T−τ)k>0 constant
An cup of coffee is served at 185∘F in a room where the temperature is 65∘F. 2 minutes later the temperature of the coffee has dropped to 155∘F.
loge3=1.09872,loge.34=0.2877
Time required for coffee to have 105∘F temperature is
View SolutionNewton's law of cooling states that the rate of change of the temperature T of an object is proportional to the difference between T and the (constant) temperature τ of the surrounding medium, we can write it as dTdt=−k(T−τ)k>0 constant
An cup of coffee is served at 185∘F in a room where the temperature is 65∘F. 2 minutes later the temperature of the coffee has dropped to 155∘F.
loge3=1.09872,loge.34=0.2877
Temperature of coffee at time t is given by
View SolutionAt 10.00 A.M. a woman took a cup of hot instant coffe from her microwave oven and placed it on a nearby Kitchen counter to cool. At this instant the temperature of the coffee was 180∘F, and 10 minutes later it was 160∘F. Assume that constant temperature of the kitchen was 70∘F.
(i) What was the temperature of the coffee at 10.15 A.M. ?
View SolutionAt 10.00 A.M. a woman took a cup of hot instant coffe from her microwave oven and placed it on a nearby Kitchen counter to cool. At this instant the temperature of the coffee was 180∘F, and 10 minutes later it was 160∘F. Assume that constant temperature of the kitchen was 70∘F.
The woman likes to drink coffe when its temperature is between 130∘F and 140∘F. between what time should she have drunk the coffee?
View Solution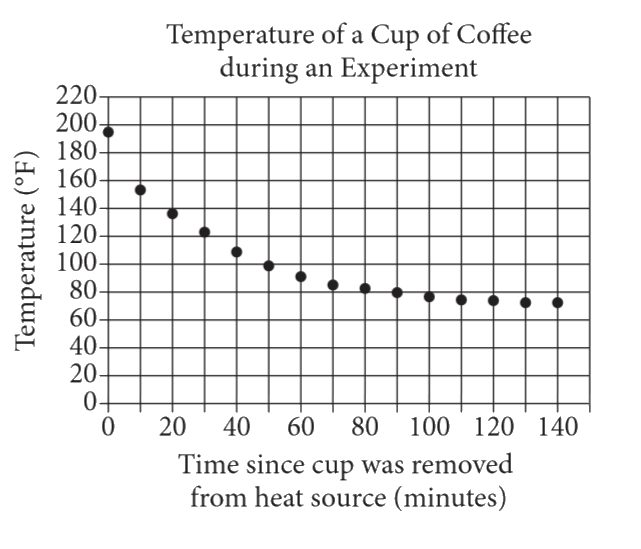
In an experiment, a heated cup of coffee is removed from a heat source, and the cup of coffee is then left in a room that is kept at a constant temperature. The graph above shows the temperature, in degrees Fahrenheit (.∘F), of the coffee immediately after being removed from the heat source and at 10-minute intervals thereafter.
Of the following, which best approximates the temperature, in degrees Fahrenheit, of the coffee when it is first removed from the heat source?
View Solution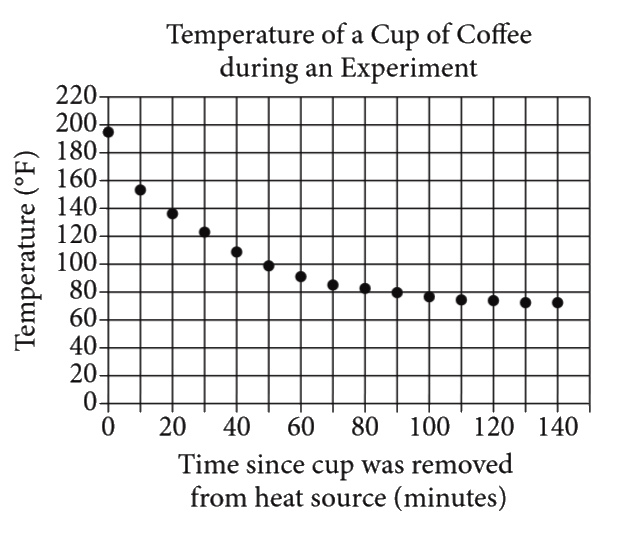
In an experiment, a heated cup of coffee is removed from a heat source, and the cup of coffee is then left in a room that is kept at a constant temperature. The graph above shows the temperature, in degrees Fahrenheit (.∘F), of the coffee immediately after being removed from the heat source and at 10-minute intervals thereafter.
During which of the following 10-minute intervals does the temperature of the coffee decrease at the greatest average rate?
View SolutionA cup of coffee cools from 150∘ F to 144∘ F in I min in a room temperature at 72∘ F. How much time with the coffee take to cool from 110∘ F to 104∘ F in the same room?
View SolutionA cup of coffee cools from 150∘F to 144∘ F m 1 min in a room at 72∘F. How much time will the coffee take to cool from 110∘F to 104∘F in the same room ?
View SolutionA cup of coffee at temperature 100∘C is placed in a room whose temperature is 20∘C and it costs to 60∘C in 10 minutes find the temperature after a further interval of 10 minutes .
View SolutionA cup of coffee at temperature 100∘C is placed in a room whose temperature is 15∘C and it cools to 60∘C in 5 minutes. Find its temperature after a further interval of 5 minutes
View Solution
