Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90∘−12A,90∘−12B and 90∘−12C
The correct Answer is:NA
NA
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90o−12A ,90o−12B and 90o−12C
View SolutionBisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at the points D,E and F respectively. Prove that angle EDF=90∘−12∠A
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionIn ABC, the three bisectors of the angle A, B and C are extended to intersect the circumcircle at D,E and F respectively. Prove that ADcosA2+BEcosB2+CFcosC2=2R(sinA+sinB+sinC)
View SolutionIf the bisector of the angel C of a triangle ABC cuts AB in D and the circumcircle E, prove that CE:DE=(a+b)2:c2
View SolutionLet the altitudes from the vertices A, B and Cof the triangle e ABCmeet its circumcircle at D, E and F respectively and z1,z2andz3 represent the points D, E and F respectively. If z3−z1z2−z1 is purely real then the triangle ABC is
View SolutionThe angles A, B and C of a triangle ABC are in arithmetic progression. If 2b2=3c2 then the angle A is :
View SolutionBisectors of interior ∠ B and exterior ∠ ACD of a ΔABC intersect at the point T. prove that ∠BTC=12∠ BAC.
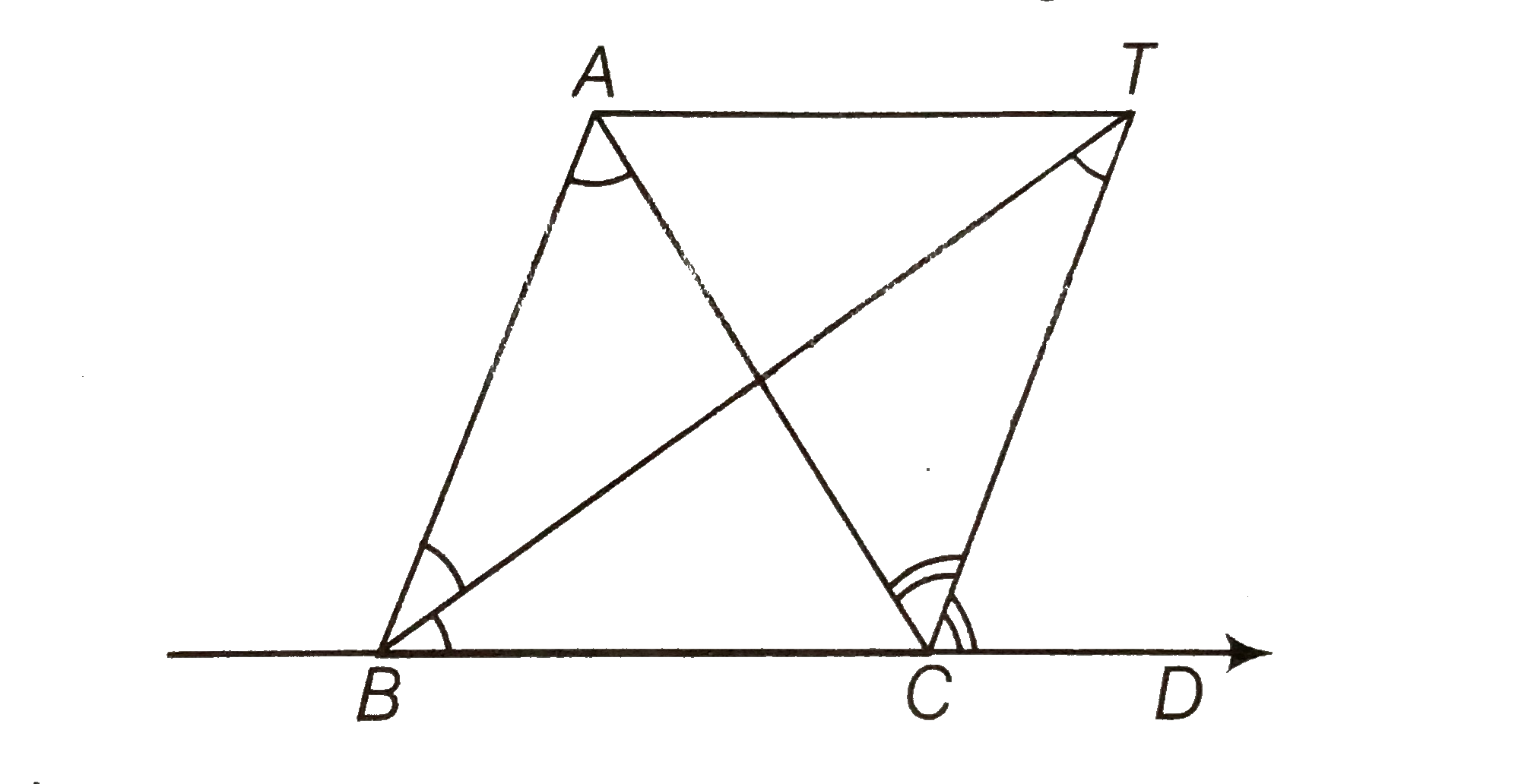
View SolutionThe internal bisectors of the angles of a triangle ABC meet the sides in D, E, and F. Show that the area of the triangle DEF is equal to 2△abc(b+c)(c+a)(a+b), where △ is the area of ABC.
View SolutionThe circumcentre of the triangle ABC is O . Prove that ∠OBC+∠BAC=90∘.
View Solution
