In Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

Step by step video & image solution for In Delta ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB and Q (shown in figure), then prove that ar (DeltaBPQ) = (1)/(2) ar (DeltaABC). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC
 View Solution
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔACD)= area (ΔABE)View SolutionIn figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
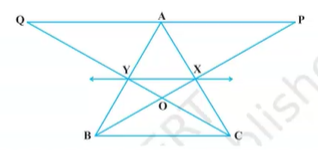 View Solution
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn the given figures, AB > AC and D is any point on BC.
Prove that : AB >AD.
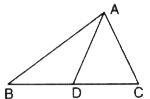 View Solution
View SolutionIn triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 , find the perimeter of the trapezium PBCQ.
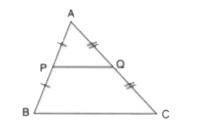 View Solution
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIn triangle ABC, M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use Intercept Theorem to show that MN bisects AD.
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.
 View Solution
View Solution

