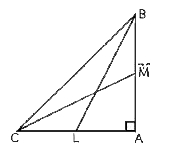
BL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2
Video Solution
Text Solution
GIVEN AΔABC in which BL and CM are medians and ∠A=90∘
TO PROOF 4(BL2+CM2)=5BC2
PROOF In ΔBAC,∠A=90∘
∴BC2=AB2+AC2 ...(i) [ by Pythagora's theorem]
In ΔBAL,∠A=90∘
∴BL2=AL2+AB2 [ by Pythagora's theorem]
⇒BL2=(12AC)2+AB2⇒BL2=14AC2+AB2
⇒4BL2=AC2+4AB2 ....(i)
In ΔCAM,∠A=90∘
∴CM2=AM2+AC2
⇒CM2=(12AB)2+AC2⇒CM2=14AB2+AC2
⇒4CM2=AB2+4AC2.
On adding (ii) and (iii), we get 4(BL2+CM2)=5(AB2+AC2)
Hence,4(BL2+CM2)=5BC2[ using (i)]
|
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
In a Δ right angled at B . AC = 5 cm , median AL=3√52 find the length of second median CM in cm ?
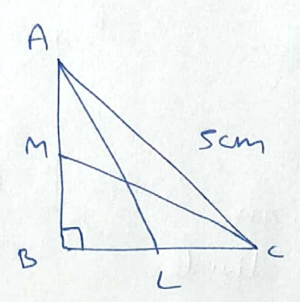 A2√5 cmB5√2 cmC10√2 cmD4√5 cm
A2√5 cmB5√2 cmC10√2 cmD4√5 cm
ABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionIn ΔABC,∠BAC=90∘, seg BL and seg CM are median of ΔABC. Then prove that: 4(Bl2+Cm2)=5BC2
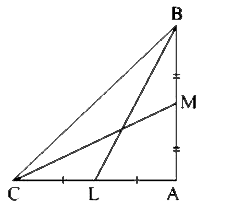
View Solutionseg AN and seg CM are the medians of △ABC in which ∠B=90∘ Prove that 4(AN2+CM2)=5AC2
View SolutionThe points A(2,9),B(a,5),C(5,5) are the vertices of a triangle ABC right angled at B . Find the value of a and hence the area of ABC.
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
View Solution