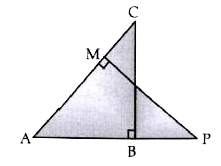
In figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
Video Solution
Text Solution
(i)In ΔABC and ΔAMP
∠BAC=∠PAM, As both angles are common.
∠ABC=∠AMP=90∘
As these two angles are equal, third angle will also be equal for these two triangles.
As, all three angles are equal, we can say that
ΔABC~ΔAMP
(ii)It also means,
ABAM=CAPA=BCMP
Hence,CAPA=BCMP
|
Similar Questions
Knowledge Check
If triangle ABC is right angled at C, then the value of sec (A+B) is
A0B1C2√3DNot definedABC is a right angled triangle. B being the right angle. Mid-points of BC and AC are respectively B' and A'. Area of ΔA'B'C' is
A12×area of ΔABCB23×area of ΔABCC14×area of ΔABCD18×area of ΔABCIf in a triangle ABC, right angled at B, s-a=3, s-c=2, then the values of a and c are respectively
A2,3B3,4C4,3D6,8
In the given figure, ΔABCandΔAMP are right- angled at B and M respectively.
Prove that (i) ΔABC≈ΔAMP
(ii)CAPA=BCMP
View Solutionif in triangle ABC right angled at C then tanA+tanB
View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively whereΔABC~ΔPQR, prove that ABPQ=ADPM
View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that:
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(ii) ΔCMB~ΔRNQ
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP
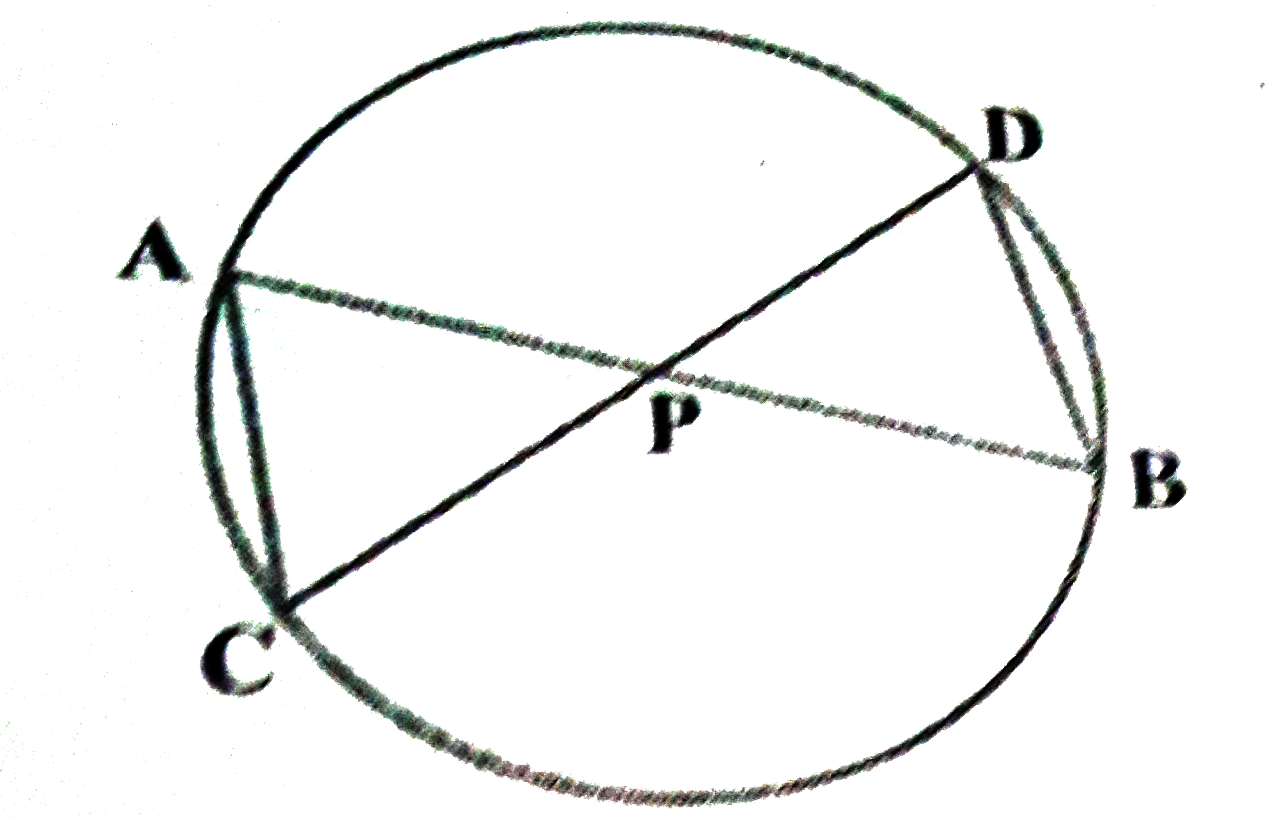
View Solution