By counting squares, estimate the area of the figure 10.9 a.
To estimate the area of the given figure by counting squares, we will follow these steps:
1. Identify Full Squares:
- Count the number of full squares in the figure. A full square is one that is completely filled.
- In this case, there is 1 full square.
Hint: Look for squares that are completely filled without any part missing.
2. Identify Half Squares:
- Count the number of squares that are exactly half filled.
- In this case, there are 0 half squares.
Hint: A half square will have exactly half of its area filled. If none are found, write down zero.
3. Identify More Than Half Squares:
- Count the number of squares that are more than half filled.
- In this case, there are 7 squares that are more than half filled.
Hint: Look for squares that have more than half of their area filled but are not completely filled.
4. Identify Less Than Half Squares:
- Count the number of squares that are less than half filled.
- In this case, there are 9 squares that are less than half filled.
Hint: These squares will have less than half of their area filled.
5. Calculate the Area:
- Use the following formula to calculate the area:
Area=(Number of Full Squares×1)+(Number of Half Squares×12)+(Number of More Than Half Squares×1)+(Number of Less Than Half Squares×0)
- Plugging in the values:
Area=(1×1)+(0×12)+(7×1)+(9×0)
- Simplifying this gives:
Area=1+0+7+0=8
Final Answer:
The estimated area of the figure is 8 square units.
- Count the number of full squares in the figure. A full square is one that is completely filled.
- In this case, there is 1 full square.
- Count the number of squares that are exactly half filled.
- In this case, there are 0 half squares.
- Count the number of squares that are more than half filled.
- In this case, there are 7 squares that are more than half filled.
- Count the number of squares that are less than half filled.
- In this case, there are 9 squares that are less than half filled.
- Use the following formula to calculate the area:
Area=(Number of Full Squares×1)+(Number of Half Squares×12)+(Number of More Than Half Squares×1)+(Number of Less Than Half Squares×0)
- Plugging in the values:
Area=(1×1)+(0×12)+(7×1)+(9×0)
- Simplifying this gives:
Area=1+0+7+0=8
The estimated area of the figure is 8 square units.
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.2
1 Videos
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.1
16 Videos
- KNOWING OUR NUMBERSBOOK - NCERT ENGLISHCHAPTER - KNOWING OUR NUMBERSEXERCISE - EXERCISE 1.3
3 Videos
- PLAYING WITH NUMBERSBOOK - NCERT ENGLISHCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.1
4 Videos
Similar Questions
Knowledge Check
The 8-sided figure below is divided into 5 congruent squares. The total area of the 5 squares is 125 square inches. What is the perimeter, in inches, of the figure?
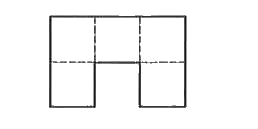 A25B60C80D100
A25B60C80D100The perimeter of square is 36 inches . What is the area of the square , in square inches ?
A6B9C18D81The area of a square is 1 sq. m Express the area of this square is sq. mm.
A1,00,00,000 sq mmB10,00,000 sq mmC1,00,000 sq mmD20,00,000 sq mm
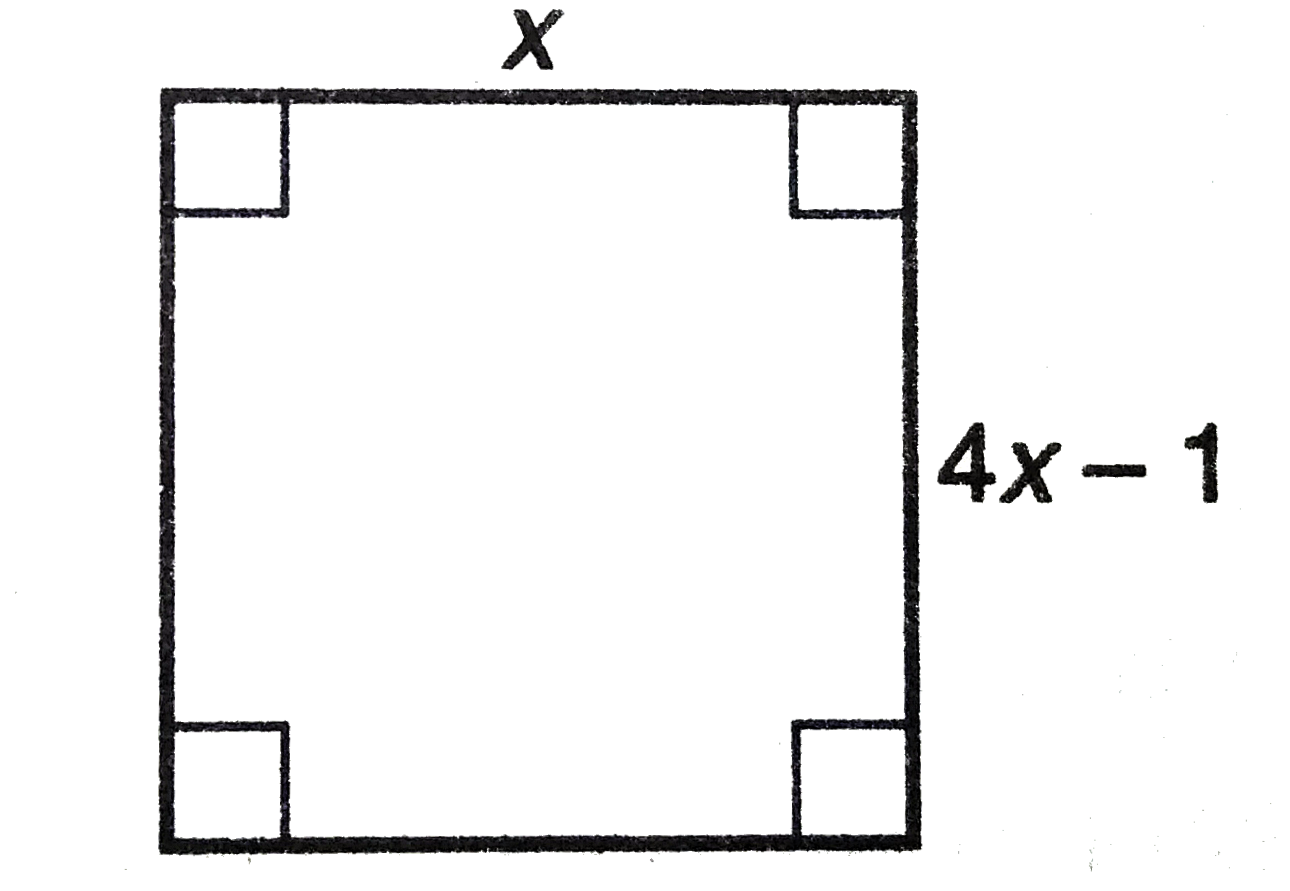
What is the area of the square above?
View SolutionDraw any circle on the graph paper. Count the squares and use them to estimate the area of the circular region.
View SolutionFind the area of the shape shown in the figure 10.10.
View Solution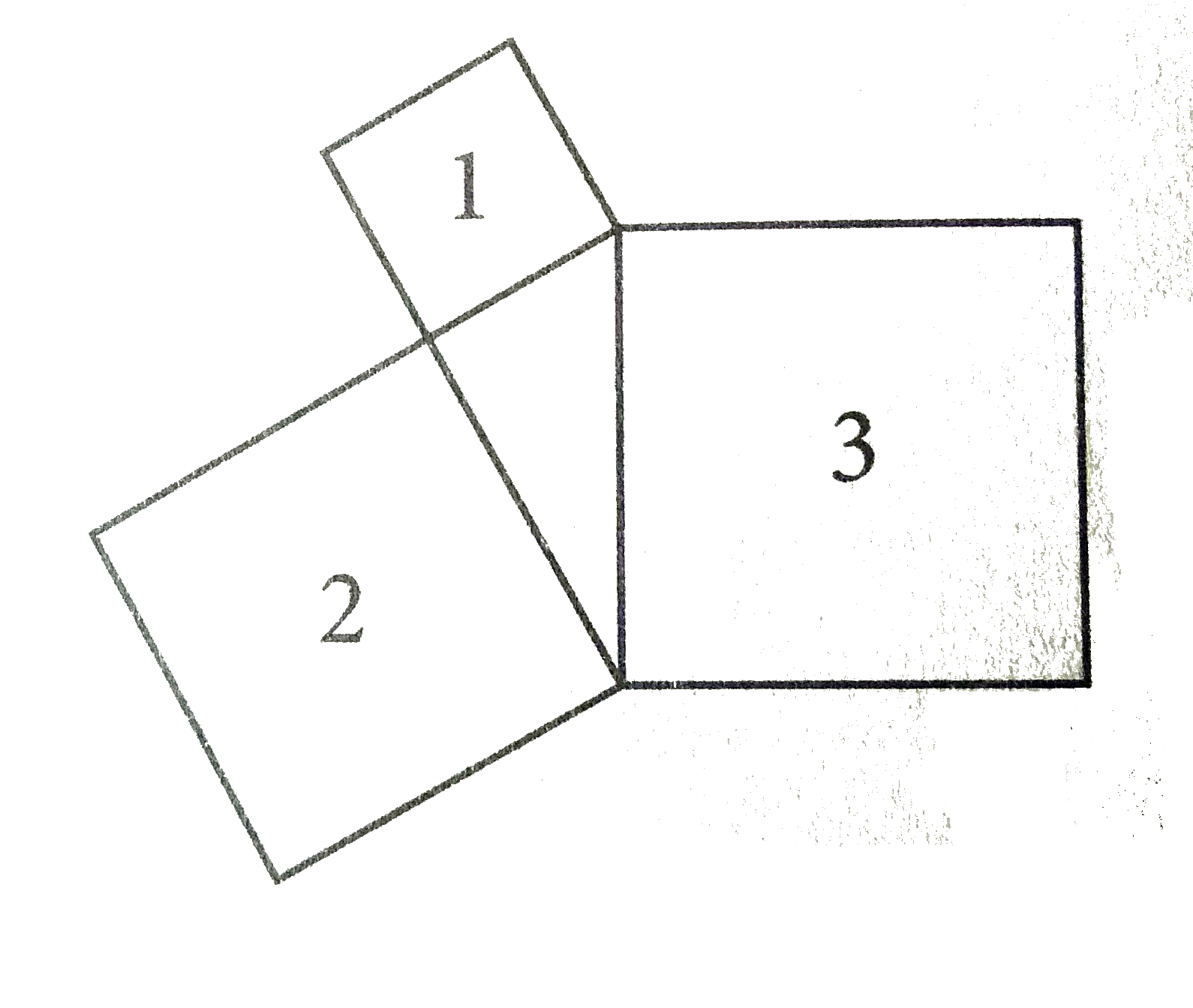
Each of the quadrilaterals figure above is a square. The area of the smallest square (square 1) is 16 square units, and the area of the medium square (square 2) is 48 square units. What is the area, in square units, of the largest square (square 3)?
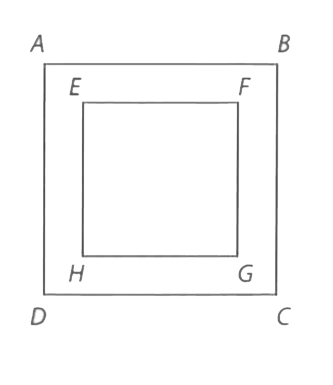
View SolutionABCD is a square picture frame (see figure). EFGH is a square inscribed within ABCD as a space for a picture. The area of EFGH (for the picture) is equal to the area of the picture frame (the area of ABCD minus the area of EFGH). If AB=6, what is the length EF ?
View Solution

