By the graphical method, find whether the following pair of equations are consistent of not. If consistent, solve them.
(i) $3 x + y + 4 = 0, 6 x - 2 y + 4 = 0$
(ii) $x - 2 y = 6, 3 x - 6 y = 0$
(iii) $x + y = 3, 3 x + 3 y = 9$

Video Solution

Text Solution

Verified by Experts

(i) Given pair of equations is
3x+y+4=0 $... (i)$
and $6 x - 2 y + 4 = 0 ... (i i)$
On comparing with $a x + b y + c = 0$ , we get
$a_{1} = 3, b_{1} = 1$
and $c_{1} = 4$ [from Eq. (i)]
$a_{2} = 6, b_{2} = - 2$
and $c_{2} = 4$ [from Eq.(ii)] $< b r > H e r e,$ (a_(1))/(a_(2))=(3)/(6)=(1)/(2) , (b_(1))/(b_(2))=(1)/(-2) $< b r > and$ (c_(1))/(c_(2))=(4)/(4)=(1)/(1) $< b r >$ :' (a_(1))/(a_(2))!=(b_(1))/(b_(2)) $< b r > S o, t h e g i v e n p a i r o f l \in e a r e q u a t i o n s a r e \int e r sec t \in g a t o \neq p \oint, ∴ t h e s e l \in e s h a v e u n i q u e s o l u t i o n . < b r > H e n c e, g i v e n p a i r o f l \in e a r e q u a t i o n s i s c o n s i s t e n t . < b r > W e h a v e, 3 x + y + 4 = 0 < b r >$ rArr " " y=-4-3x $< b r > w h e n x = 0, t h e n y = - 4 < b r > w h e n x = - 1, t h e n y = - 1 < b r > W h e n x = - 2, t h e n y = 2 < b r >$ {:(" "x,0,-1,-2),(" "y,-4,-1,2),("Points","B","C","A"):} $< b r > and 6 x - 2 y + 4 = 0 < b r >$ rArr 2y=6x+4 $< b r >$ rArr y=3x+2 $< b r > W h e n x = 0, t h e n y = 2 < b r > W h e n x = - 1, t h e n y = - 1 < b r > W h e n x = 1, t h e n y = 5 < b r >$ {:(" "x,-1,0,1),(" "y,-1,2,5),("Points","C","Q","P"):} $< b r > P l o \in g t h e p \oint B (0, - 4) and A (- 2, 2), w e \geq t t h e s t r a i g h t l \in e A B . P l o \in g t h e p \oint s Q (0, 2) and P (1, 5), w e \geq t t h e s t r a i g h t l \in e P Q . T h e l \in e s A B and P Q \int e r sec t a t C (- 1, - 1) . < b r > < i m g a \leq ocr_image l o a d \in g = lazy s r c = https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_NCERT_EXE_MATH_X_C03_S01_030_S01.png w h = 80% mx-auto s t y \leq = background:white; > < b r > (i i) G i v e n p a i r o f e q u a t i o n s i s$ " " x-2y=6 " " ...(i) $< b r > and$ " " 3x-6y=0 " " ...(ii) $< b r > O n c o m p a r \in g w i t h a x + b y + c = 0 . w e \geq t < b r >$ a_(1)=1, b_(1)=-2 $and$ c_(1)=-6 " " $[o m E q . (i)] < b r >$ a_(2)=3, b_(2)=-6 $and$ c_(2)=0 $[from Eq. (i i)] < b r > H e r e,$ (a_(1))/(a_(2))=(1)/(3), (b_(1))/(b_(2))= (-2)/(-6)=(1)/(3) $and$ (c_(1))/(c_(2))=(-6)/(0) $< b r >$ :. " " (a_(1))/(a_(2))=(b_(1))/(b_(2))=(c_(1))/(c_(2)) $< b r > H e n c e, t h e l \in e s r e p r e s e n t e d b y t h e g i v e n e q u a t i o n s a r e p a r a l \leq l . T h e r e f or e, i t h a s n o s o l u t i o n . S o, t h e g i v e n p a i r o f l \in e s i s \in c o n s i s t e n t . < b r > (i i i) G i v e n p a i r o f e q u a t i o n i s$ " " x+y=3 " " ...(i) $< b r > and$ " " 3x+3y=9 " " ...(ii) $< b r > O n c o m p a r \in g w i t h a x + b y + c = 0 . w e \geq t < b r >$ a_(1)=1, b_(1) $and$ c_(1)=-3 " " $[o m E q . (i)] < b r >$ a_(2)=3, b_(2)=3 $and$ c_(2)=-9 " " [from Eq. (ii)]
Here, $\frac{a_{1}}{a_{2}} = \frac{1}{3}, \frac{b_{1}}{b_{2}} = \frac{1}{3}$ and $\frac{c_{1}}{c_{2}} = \frac{- 3}{- 9} = \frac{1}{3}$
$\Rightarrow \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$
So, the given pair of lines is coincident. Therefore, these lines have infinitely many solutions. Hence, the given pair of linear equations is consistent.
Now, $x + y = 3 \Rightarrow y = 3 - x$
If x=0, then y=3, If x=3, then y=0
$\begin{matrix} x & 0 & 3 y & 3 & 0 Points & A & B \end{matrix}$
and $3 x + 3 y = 9 \Rightarrow 3 y = 9 - 3 x$
$\Rightarrow y \frac{9 - 3 x}{3}$
If x=0, then y=3, if x=1, then y=2 and if x=3, then y=0
$\begin{matrix} x & 0 & 1 & 3 y & 3 & 2 & 0 Points & C & D & E \end{matrix}$

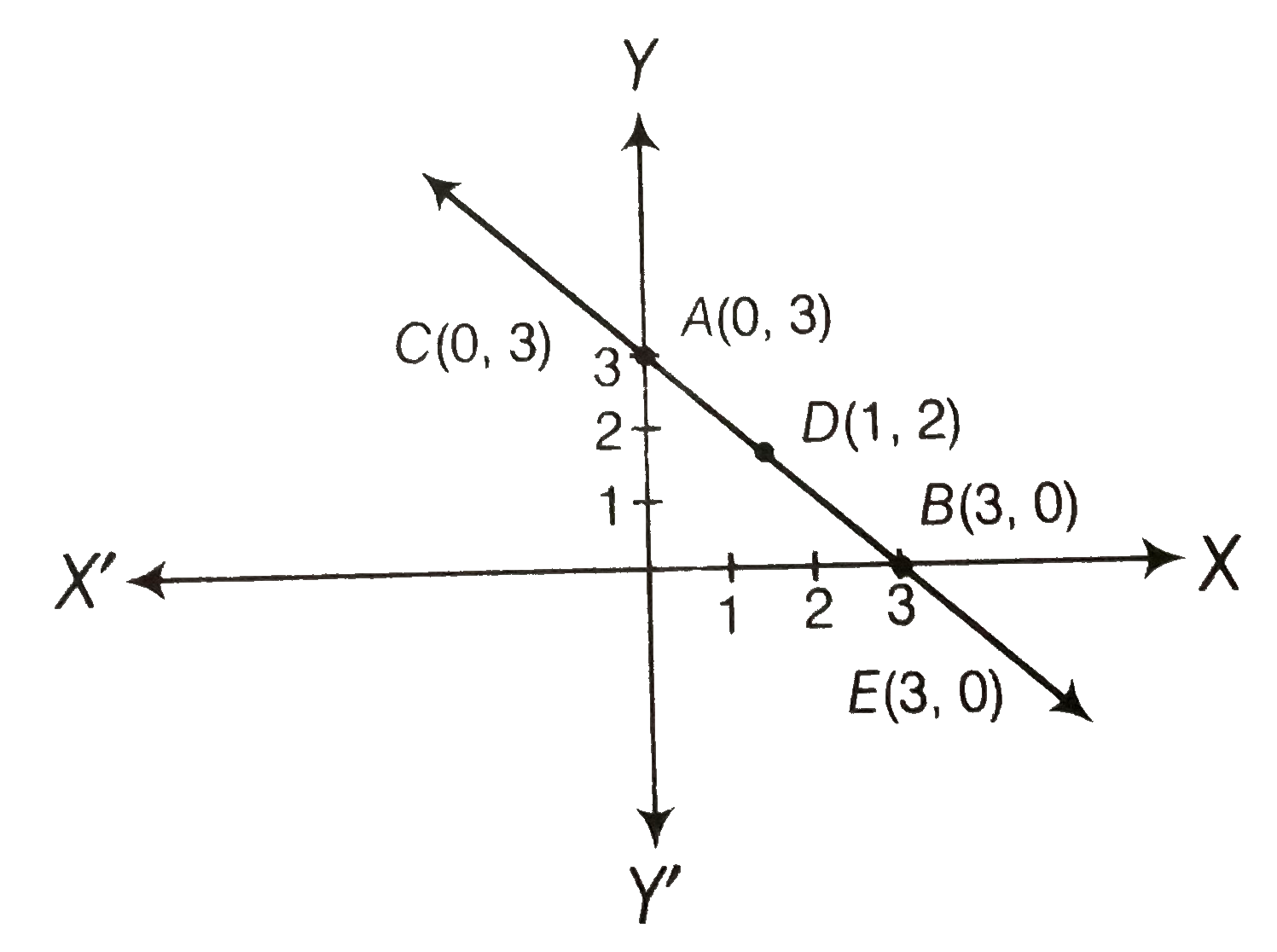
Plotting the points A (0,3) and B (3,0), we get the line AB. Again, plotting the points C(0,3)D(1,2) and E(3,0), we get the line CDE.
We observe that the lines represented by Eqa. (i) and (ii) are coincident.

|

Updated on:21/07/2023

Class 10 MATHS LINEAR EQUATIONS IN TWO VARIABLE

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR-PAIR OF LINEAR EQUATIONS IN TWO VARIABLES-Exercise 3.3 Short Answer Type Questions

Home
Ask Doubt
Profile