Centre of the circle is (a, b) . If (0,3) and (2,0) are two points on a circle , then find the relation between a and b .
A
4a−6b−5=0
B
4a + 6 b - 5 = 0
C
−4a+5=0
D
4a−6b+5=0
Video Solution
Text Solution
The correct Answer is:D
The distance from centre of the circle to any point on th circle is its radius.
|
Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 2
21 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Eassy Type Questions
5 Videos
- BANKING AND COMPUTINGBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING AND COMPUTINGEXERCISE - Level 3
6 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - CONCEPT APPLICATION
61 Videos
Similar Questions
Knowledge Check
Centre of circle , passing through (0,0) ,(a,0) and (0,b) , is
A(b2,a2)B(a2,b2)C(b,a)D(a,b)A chord of the circle x2+y2=a2 cuts it at two points A and B such that ∠AOB=π/2, where O is the centre of the circle. If there is a moving point P on this circle, then the locus of the orthocentre of ΔPAB will be a
AparabolaBcircleCstraight lineDnone of thesePA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘
If the points A(4, 3) and B(x, 5) lie on a circle with the centre O(2, 3), find the value of x.
View Solution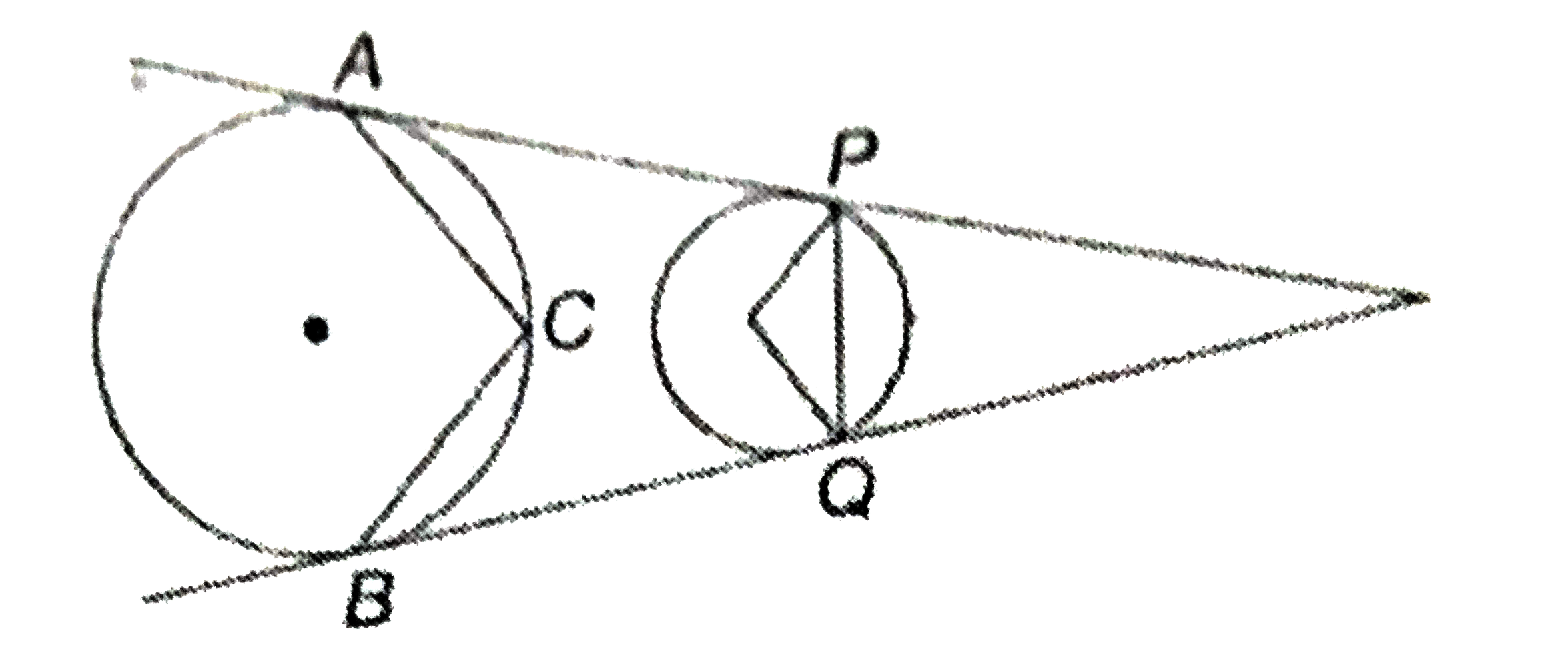
In the diagram above, A,B,P and Q are points of contacts of direct common tangents of the two circles. If ∠ACB is 120∘ , then find the angle between the two tangents and angle made by PQ at the centre of same circle.
View SolutionIn the circle with centre O and A,B,C are the points on the circle, ∠AOB=60∘. Find ∠ACB
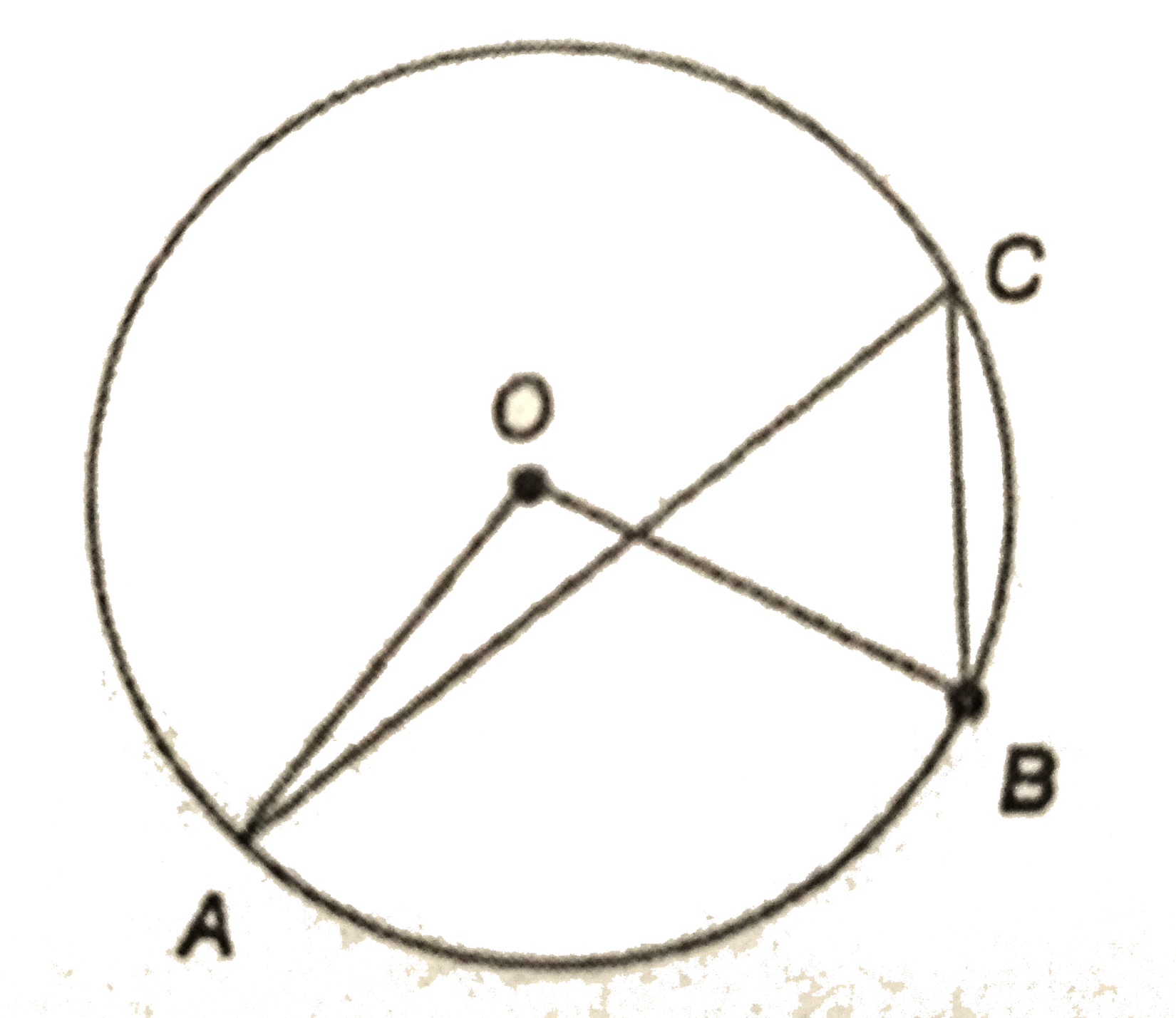
View SolutionA circle passes through (0,0) and (1,0) and touches the circle x2+y2=9 then the centre of circle is -
View SolutionIf the line 2x−y+1=0 touches the circle at the point (2,5) and the centre of the circle lies in the line x+y−9=0. Find the equation of the circle.
View Solution
