Circle passes through the centre of circle and is tangential to it. If the area of is , then the area of is _______
The correct Answer is:C
To solve the problem, we need to find the area of circle C2 given that circle C1 passes through the center of circle C2 and is tangential to it. We also know that the area of circle C1 is 4cm2.
1. Find the Radius of Circle C1:
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle. Given that the area of circle C1 is 4cm2, we can set up the equation:
πr21=4
To find r1, we rearrange the equation:
r21=4π
Taking the square root:
r1=√4π=2√π
2. Understanding the Relationship between the Two Circles:
Circle C1 passes through the center of circle C2 and is tangential to it. This means that the distance from the center of circle C2 to the edge of circle C1 is equal to the radius of circle C2 (denote it as r2).
The distance from the center of circle C2 to the edge of circle C1 is equal to the radius of circle C1 plus the radius of circle C2:
r1+r2=r2
Rearranging gives:
r2=r1
3. Finding the Radius of Circle C2:
Since we have established that r2=r1, we substitute the value of r1:
r2=2√π
4. Calculate the Area of Circle C2:
Now we can find the area of circle C2 using the area formula:
A2=πr22
Substituting r2:
A2=π(2√π)2=π⋅4π=4cm2
Thus, the area of circle C2 is 4cm2.
Final Answer:
The area of C2 is 4cm2.
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle. Given that the area of circle C1 is 4cm2, we can set up the equation:
πr21=4
To find r1, we rearrange the equation:
r21=4π
Taking the square root:
r1=√4π=2√π
Circle C1 passes through the center of circle C2 and is tangential to it. This means that the distance from the center of circle C2 to the edge of circle C1 is equal to the radius of circle C2 (denote it as r2).
r1+r2=r2
Rearranging gives:
r2=r1
Since we have established that r2=r1, we substitute the value of r1:
r2=2√π
Now we can find the area of circle C2 using the area formula:
A2=πr22
Substituting r2:
A2=π(2√π)2=π⋅4π=4cm2
The area of C2 is 4cm2.
Topper's Solved these Questions
- IMO QUESTION PAPER 2019 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET BEXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO QUESTION PAPER 2019 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2019 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET AEXERCISE - Achievers section
5 Videos
- IMO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section
5 Videos
Similar Questions
A circle C1 passes through the centre of the circle C2;x2+y2=4 and gets bisected at its point of intersection with C2 .The radius of c1 is equal to:
View SolutionC1 and C2 are circle of unit radius with centers at (0, 0) and (1, 0), respectively, C3 is a circle of unit radius. It passes through the centers of the circles C1andC2 and has its center above the x-axis. Find the equation of the common tangent to C1andC3 which does not pass through C2.
View Solution
Knowledge Check
Statement-1: The centre of the circle passing through the points (0, 0), (1, 0) and touching the circle C:x2+y2=9 lies inside the circle.
Statement-2: If a circle C1 passes through the centre of the circle C2 and also touches the circle, the radius of the circle C2 is twice the radius of circle C1AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is not a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.A circle has its total area A. there are four equal circle tangent to this circle passing through the centre of this circle and tangent to this circle. The area of each such circle is B. the area of each region that is created by overlapping of any two of these circles is D and the area of each region that is not covered by these circles within the larger circle is C. if D=π25, find the value of C.
A2π25Bπ5√5Cπ49Dnone of theseThe circle C1 of radius (√3+1) has chord AB which touch another circle C2 which is concentric to C1. If radius of C2 is (√3−1) then length of AB (in cm) will be.
A24√3cmB8√3cmC44√3cmD4√4cm
If radius of circle C1 is 2 times the radius of circle C2, then ratio of area C1 to that of C2 is
View SolutionIn the given figure, triangle ABC is drawn such that AB is tangent to a circle at A whose radius is 10 cm and BC passes through centre of the circle. Point C lies on the circle. If BC = 36 cm and AB 24cm,then what is the area (in cm2) of triangle ABC?
View SolutionIn the given figure, ΔPQR is drawn such that PQ is tangent to a circle whose radius is 10 cm and QR passes through centre of the circle. Point R lies on the circle. If QR=36cm, then what is the area (in cm2 ) of ΔPQR ?
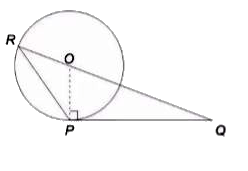
View SolutionIf C1,C2,C3,... is a sequence of circles such that Cn+1 is the director circle of Cn. If the radius of C1 is 'a', then the area bounded by the circles Cn and Cn+1, is
View SolutionIf circle C passing through the point (2, 2) touches the circle x2+y2+4x−6y=0 externally at the point (1, 1), then the radius of C is:
View Solution
