Complete solution set of inequlaity (x+2)(x+3)(x−2)(x−3)≤1
A
(−∞,0)
B
(−∞,0]∪(2,3)
C
[2,3]
D
(−∞,2)∪(3,∞)
Video Solution
Text Solution
The correct Answer is:B
(x+2)(x+3)(x−2)(x−3)≤1
⇒x2+5x+6x2−5x+6−1≤0
⇒10x(x−2)(x−3)≤0
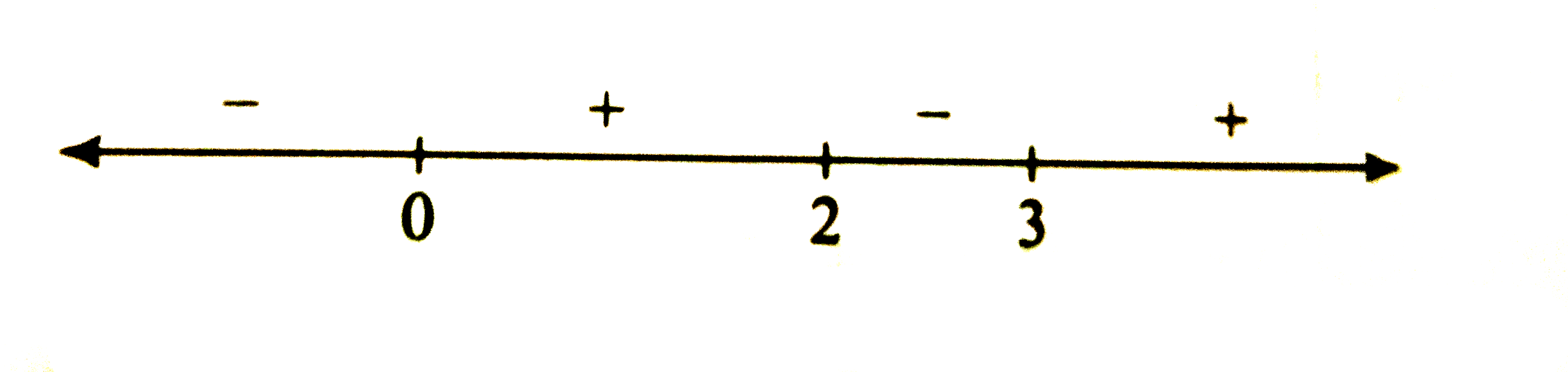
x∈(−∞,0]∪(2,3)
|
Topper's Solved these Questions
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archieves
1 Videos
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Exercise 1.5
12 Videos
- SEQUENCE AND SERIESBOOK - CENGAGECHAPTER - SEQUENCE AND SERIESEXERCISE - Question Bank
36 Videos
- SETS AND RELATIONSBOOK - CENGAGECHAPTER - SETS AND RELATIONSEXERCISE - Question Bank
15 Videos
Similar Questions
Knowledge Check
The complete solution set of inequality (x−5)1005(x+8)1008(x−1)x1006(x−2)3(x−3)5(x−6)(x+9)1010≤0
A(−∞,−9)∪(−8,0)∪(0,1)∪(2,3)∪[5,6]B(−∞,−9)∪(−9,0)∪(0,1)∪(2,3)∪[5,6)C(−∞,−9)∪(−9,0)∪(0,1]∪(2,3)∪[5,6)D(−∞,0)∪(0,1]∪(2,3)∪[5,6)]Complete solution set of the inequality ∣∣x2−x−2∣∣+|x+1|≤0 is
A(−∞,−1)B(−1,0)C{−1,0}D{−1}The solution set of inequality
(ex−1)(2x−3)(x2+x+2)(sinx−2)(x+1)x≤0A[32,∞)B(−∞,−1)∪[32,∞)C(−1,0)∪[32,∞)DR−{0,−1}
The complete solution set of the inequality x4−3x3+2x2x2−x−30≥0 is
View SolutionFind the solution set of inequality ∣∣∣3|x|−2|x|−1∣∣∣≥2.
View SolutionThe solution set of the equation x23+x13=2
View SolutionComplete solution set of ∣∣∣x2x−1∣∣∣≤1 is
View SolutionThe solution set of the inequality
2(4x−1)≤3(x+4) is
View Solution
