Complete the following magic square by supplying the missing numbers: (Figure)
To complete the magic square, we need to find the missing numbers A, B, and C such that the sum of each row, column, and diagonal equals the same total. In this case, we will find that total to be 15.
1. Identify the Total Sum:
The magic square's total sum can be determined from the known numbers in the diagonals. We can see that one diagonal has the numbers 6, 5, and 4. Therefore, the total sum is:
6+5+4=15
2. Set Up the Equations:
We will set up equations based on the rows, columns, and diagonals that include the missing numbers A, B, and C.
- For the first row:
6+B+8=15
- For the second row:
7+5+C=15
- For the diagonal from top left to bottom right:
A+5+8=15
3. Solve for B:
From the first equation:
6+B+8=15
Simplifying gives:
14+B=15
Therefore:
B=15−14=1
4. Solve for C:
From the second equation:
7+5+C=15
Simplifying gives:
12+C=15
Therefore:
C=15−12=3
5. Solve for A:
From the third equation:
A+5+8=15
Simplifying gives:
A+13=15
Therefore:
A=15−13=2
6. Fill in the Magic Square:
Now that we have the values:
- A = 2
- B = 1
- C = 3
We can fill in the magic square:
618753254
Final Values:
- A = 2
- B = 1
- C = 3
The magic square's total sum can be determined from the known numbers in the diagonals. We can see that one diagonal has the numbers 6, 5, and 4. Therefore, the total sum is:
6+5+4=15
We will set up equations based on the rows, columns, and diagonals that include the missing numbers A, B, and C.
6+B+8=15
- For the second row:
7+5+C=15
- For the diagonal from top left to bottom right:
A+5+8=15
From the first equation:
6+B+8=15
Simplifying gives:
14+B=15
Therefore:
B=15−14=1
From the second equation:
7+5+C=15
Simplifying gives:
12+C=15
Therefore:
C=15−12=3
From the third equation:
A+5+8=15
Simplifying gives:
A+13=15
Therefore:
A=15−13=2
Now that we have the values:
- A = 2
- B = 1
- C = 3
618753254
- A = 2
- B = 1
- C = 3
Topper's Solved these Questions
Similar Questions
Find the missing number:
View SolutionObserve the following pattern and supply the missing numbers. (i) 11^2 = 121 (ii) 101^2 = 10201 (iii) 1001^2 = 1002001 (iv) 100001^2 = 1___2___1 (v) 10000001^2 = _________
View SolutionFill in the missing numbers : 14/21 = □/3 = 6/□
View SolutionObserve the following pattern and supply the missing numbers. 112=1211012=10201101012=10203020110101012=.........2=10203040504030201
View SolutionHere are two different factor trees for 60. Write the missing numbers: (Figure) Figure (ii) Figure
View SolutionComplete each of the following figures along the line of symmetry.
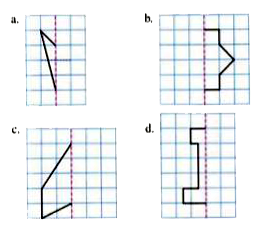 .View Solution
.View SolutionComplete the missing reactants :
(a)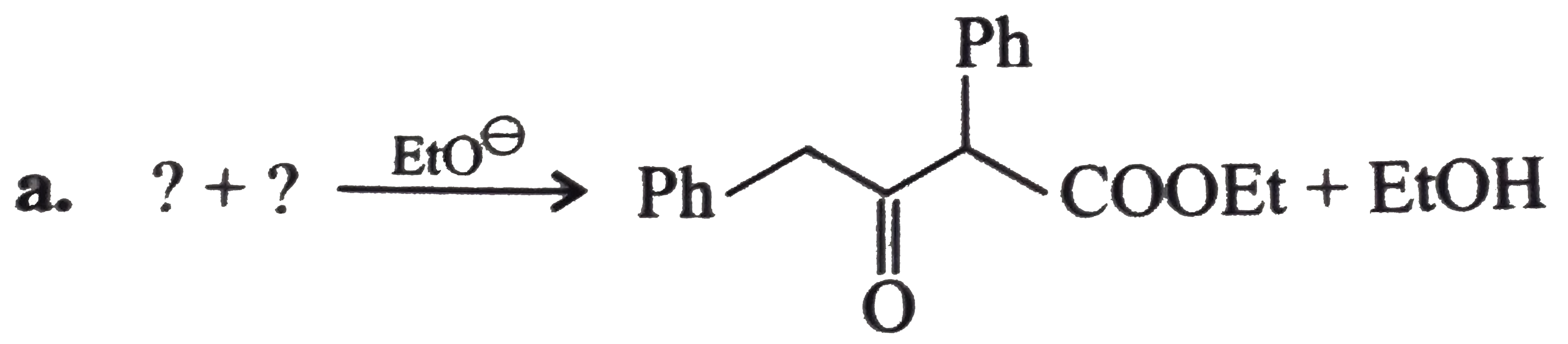 View Solution
View SolutionComplete the following the following missing reagents :
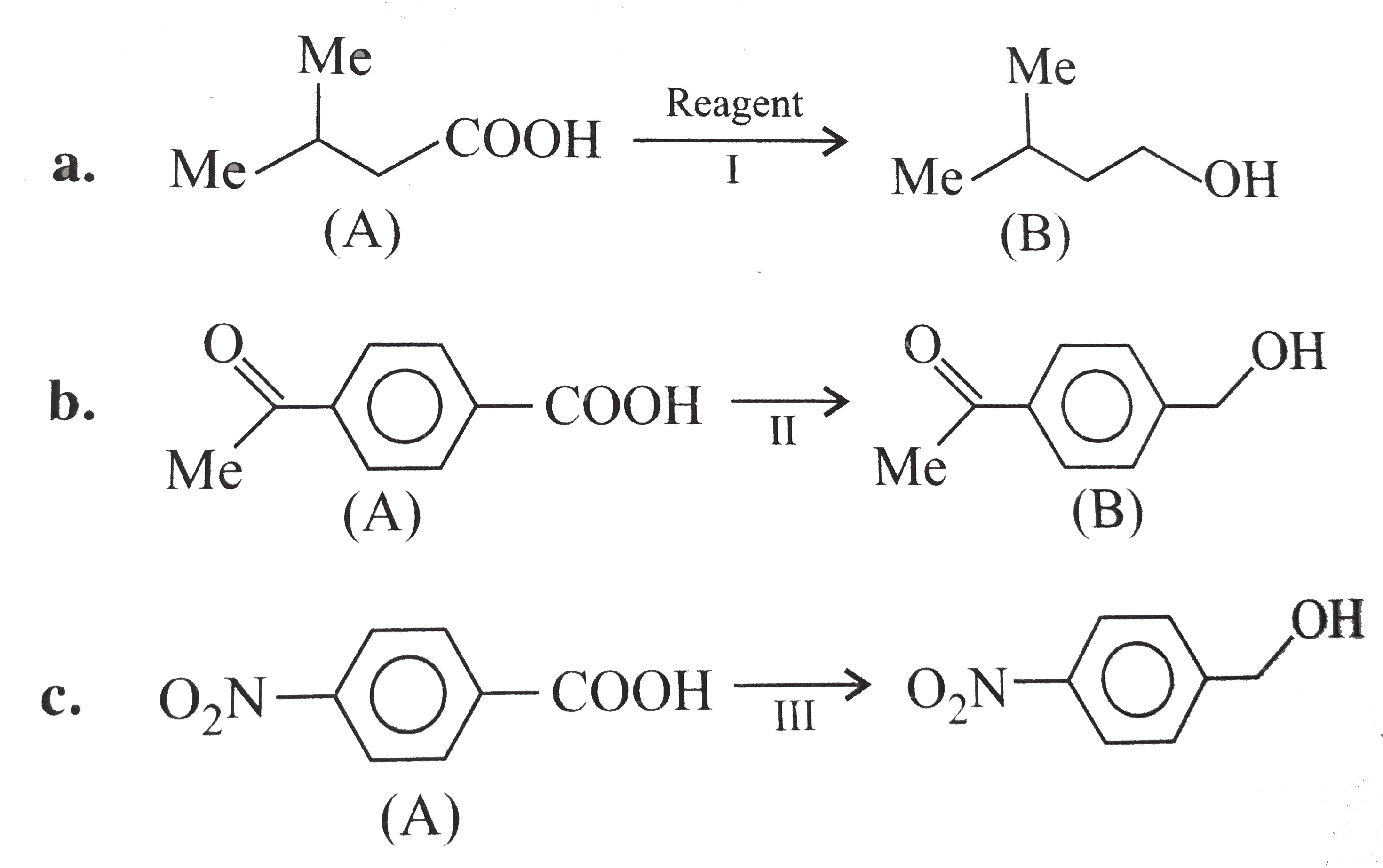
(b)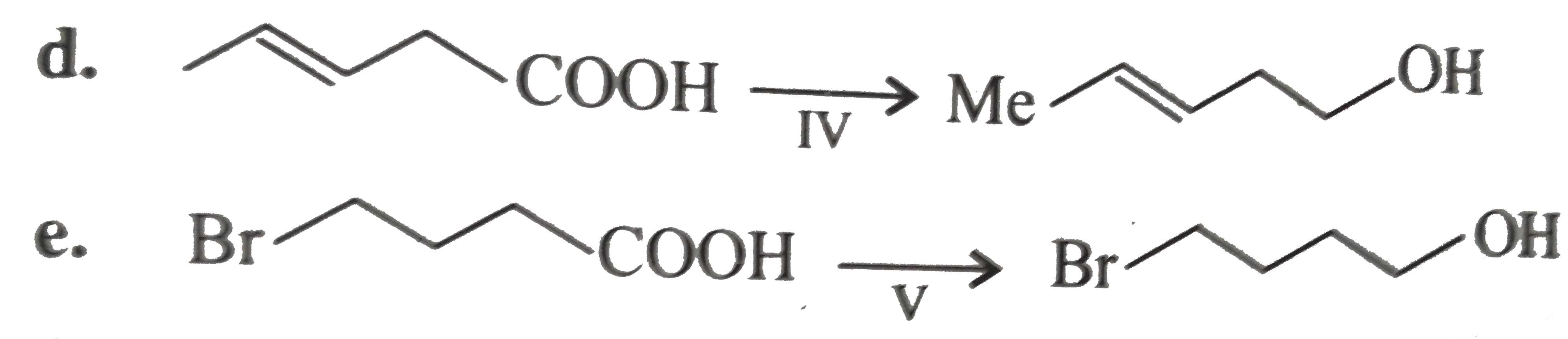 View Solution
View SolutionYou have to show that . In the following proof, supply the missing reasons
View SolutionWhich of the following has magic number of neutrons?
View Solution

